Welcome to our comprehensive guide on Algebra 2 Unit 7 Exponential and Logarithmic Functions. In this article, we will be providing you with the answers and explanations for various problems and exercises related to exponential and logarithmic functions. This unit is an important part of algebra 2, as it introduces you to the concepts and applications of exponential and logarithmic functions, which are widely used in various branches of mathematics, science, and finance.
Exponential functions are functions of the form f(x) = a^x, where a is a positive constant. These functions have a unique property that the output grows or decays at an exponential rate as the input increases or decreases. Logarithmic functions, on the other hand, are the inverse of exponential functions. They are functions of the form f(x) = log_a(x), where a is a positive constant. Logarithmic functions help us solve exponential equations and provide a way to represent the growth or decay rate of exponential functions.
Throughout this unit, you will learn how to solve problems involving exponential and logarithmic functions, including graphing them, finding their domain and range, solving exponential and logarithmic equations, and exploring real-world applications. By understanding and mastering these concepts, you will not only enhance your algebraic skills but also gain a deeper insight into the nature of growth and decay phenomena that occur in various natural and artificial systems.
Algebra 2 Unit 7 Exponential and Logarithmic Functions Answers
In Algebra 2 Unit 7, students learn about exponential and logarithmic functions and their properties. They explore how these functions can be used to model and solve real-world problems. This unit introduces students to the concept of exponential growth and decay and how to create and interpret exponential models. They also learn about logarithmic functions and how they are related to exponential functions.
One of the key topics covered in Unit 7 is solving exponential and logarithmic equations. Students learn various methods to solve these equations, such as using properties of logarithms or applying the change of base formula. They practice solving equations with different bases and exponents, as well as solving logarithmic equations involving multiple terms.
Another important concept covered in this unit is the exponential and logarithmic functions graphing. Students learn to graph exponential and logarithmic functions by identifying key points, such as the y-intercept and asymptotes. They also explore the transformations of these functions and how they affect the graph.
Overall, Algebra 2 Unit 7 provides students with a solid foundation in exponential and logarithmic functions. By understanding and applying the properties of these functions, students can solve a wide range of mathematical problems and analyze real-world situations. The answers to the exercises and problems in this unit help students check their understanding and reinforce their learning.
Understanding Exponential Functions
An exponential function is a mathematical expression in which a variable is raised to a power. It can be represented in the form of (f(x) = a cdot b^x), where (a) and (b) are constants, and (x) is the variable. Exponential functions are widely used to model various real-life situations, such as population growth, compound interest, and radioactive decay.
Properties of Exponential Functions:
- Constant base: The base (b) remains constant throughout the function, determining the rate of growth or decay.
- Increasing or decreasing: If the base (b) is greater than 1, the function exhibits exponential growth. On the other hand, if the base (b) is between 0 and 1, the function shows exponential decay.
- Asymptotic behavior: Exponential functions approach a horizontal asymptote as (x) approaches positive or negative infinity. The position of the asymptote depends on the value of (a) in the function.
Applications of Exponential Functions:
Exponential functions have numerous applications in different fields:
- Finance: Exponential functions are used to calculate compound interest, investment growth, and mortgage payments.
- Biology: Exponential functions can model population growth and disease spread.
- Physics: Exponential functions describe phenomena like radioactive decay and energy dissipation.
- Economics: Exponential functions are used to analyze economic growth, inflation rates, and stock market trends.
Graphing Exponential Functions:
Graphing exponential functions helps in visualizing their behavior and analyzing their properties. By plotting points or using technology, we can observe the shape of the function, the position of the asymptote, and the domain and range of the function. Understanding the graph of an exponential function is essential for interpreting real-world situations.
Properties of Exponential Functions
Exponential functions are a type of mathematical function that can be represented by the general form: f(x) = a^x, where a is a positive constant called the base. These functions have several key properties that make them unique and important in various applications.
1. Growth and Decay: One of the main characteristics of exponential functions is their ability to model both growth and decay. When the base a is greater than 1, the function exhibits exponential growth, meaning it increases rapidly as x increases. On the other hand, when the base a is between 0 and 1, the function shows exponential decay, decreasing rapidly as x increases.
2. Asymptotic Behavior: Exponential functions exhibit asymptotic behavior, meaning they approach but never reach a specific value as x tends to positive or negative infinity. When a is greater than 1, exponential functions approach positive infinity as x increases, while when a is between 0 and 1, they approach 0.
3. Properties of Exponents: Exponential functions follow certain rules of exponents. For example, when multiplying exponential expressions with the same base, the exponents are added: a^x * a^y = a^(x+y). Similarly, when dividing exponential expressions with the same base, the exponents are subtracted: a^x / a^y = a^(x-y).
4. Inverse Relationship: Exponential functions and logarithmic functions are inverse of each other. If we let y = f(x) = a^x, then the inverse function y = log_a(x) represents the logarithm base a of x. In other words, exponential functions and logarithmic functions “undo” each other, allowing us to solve equations involving exponents and logarithms.
In conclusion, exponential functions have distinct characteristics that set them apart from other types of functions. They can represent both growth and decay, exhibit asymptotic behavior, follow specific rules of exponents, and have an inverse relationship with logarithmic functions. Understanding these properties is essential for solving problems involving exponential functions and applying them in various fields such as economics, biology, and finance.
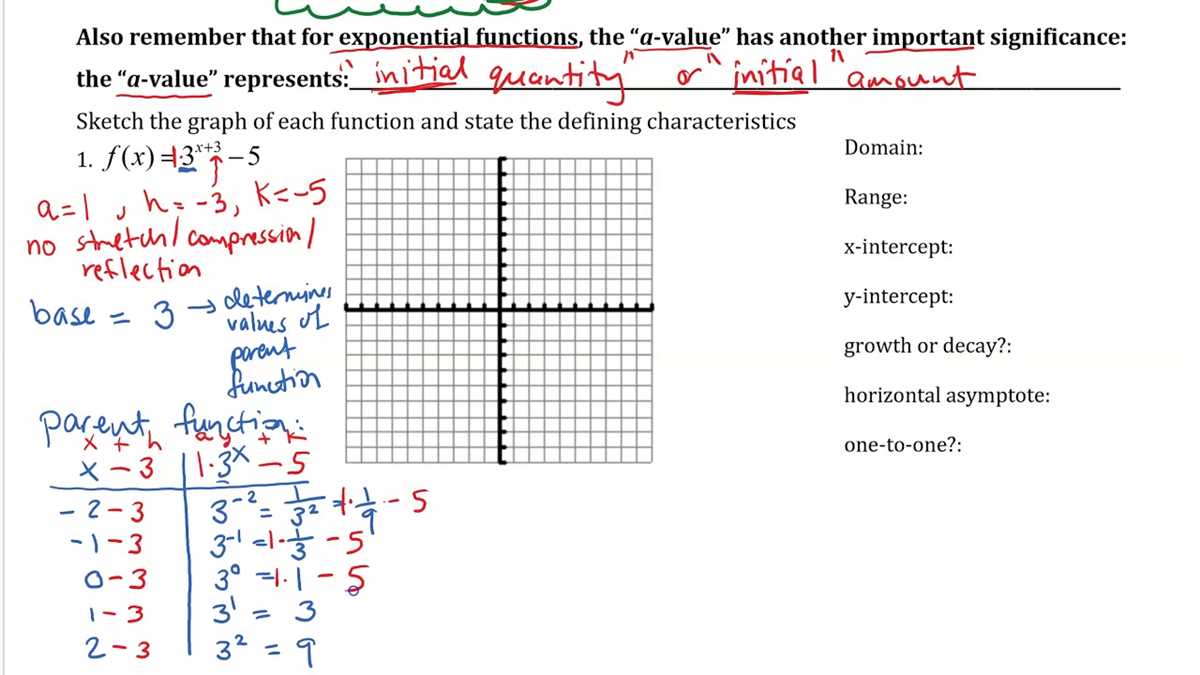
Solving Exponential Equations

Solving exponential equations involves finding the value of the variable that makes the equation true. These equations can be solved using a variety of methods, depending on the complexity of the equation. In general, the strategy for solving exponential equations includes isolating the variable and using properties of exponents.
An exponential equation typically has the form ax = b, where a and b are constants and x is the variable. To solve this type of equation, we often take the logarithm of both sides. By using the property logb(ax) = x * logb(a), we can rewrite the equation as x = logb(b).
When solving exponential equations, it is important to consider the domain of the logarithmic function. In some cases, the equation may have no solution if the base of the exponential function is negative or less than 1. Additionally, extraneous solutions may occur, so it is crucial to check the solutions obtained to ensure they satisfy the original equation.
Solving exponential equations is an essential skill in algebra and has a wide range of applications in various fields such as finance, population growth, and radioactive decay. With practice and understanding of the properties of exponents and logarithms, it is possible to successfully solve these types of equations and use them to model real-world situations.
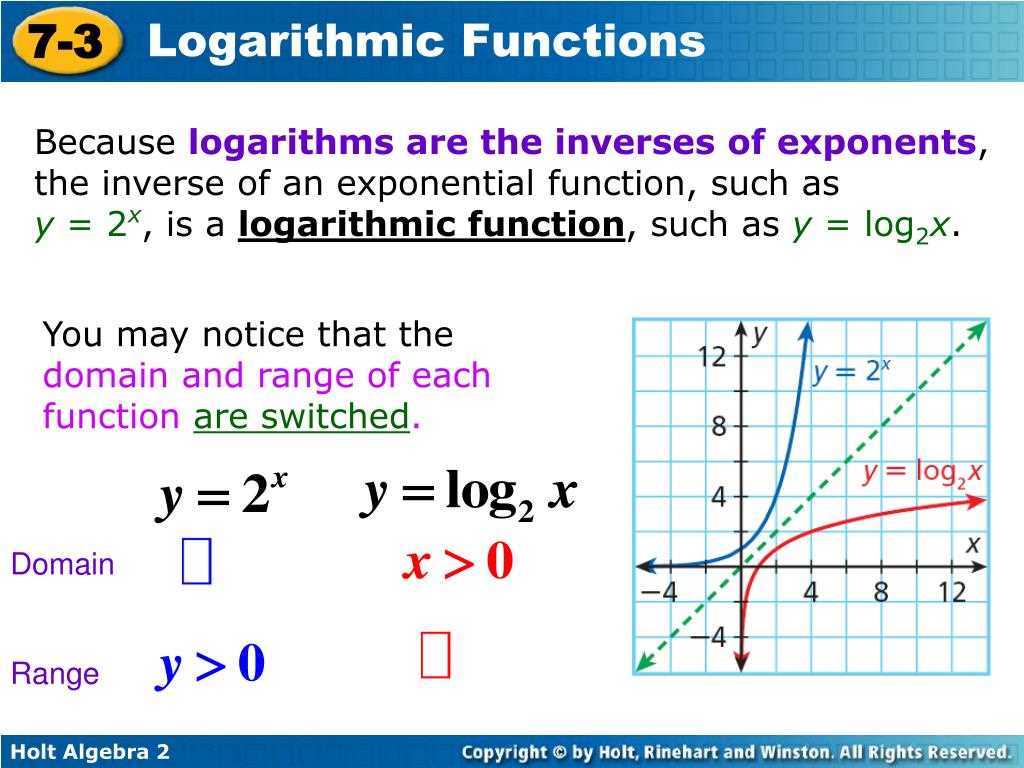
Logarithmic Functions and Their Properties

Logarithmic functions are the inverse of exponential functions. They can be written in the form y = logb(x), where b is the base and x is the argument. Logarithmic functions have several important properties that make them useful in solving a variety of mathematical problems.
One of the fundamental properties of logarithmic functions is the ability to rewrite them in exponential form. If y = logb(x), then x = by. This property can be used to simplify logarithmic expressions and solve equations involving logarithmic functions.
Logarithmic functions also exhibit certain key behaviors. For example, the graph of a logarithmic function with base b will pass through the point (1, 0). As the argument x approaches 0, the value of the logarithmic function becomes increasingly negative. On the other hand, as the argument x approaches infinity, the value of the logarithmic function becomes increasingly positive. This behavior is reflected in the shape of the logarithmic function’s graph, which resembles a curve that approaches but never reaches the x-axis.
Logarithmic functions are widely used in various fields of science, engineering, and finance. They provide a way to express exponential growth or decay in a more manageable and interpretable form. They also play a role in data analysis and modeling, as they can transform skewed data into a more symmetrical distribution, making it easier to analyze and make predictions.
- Key Properties of Logarithmic Functions:
- Inverse of Exponential Functions: Logarithmic functions are the inverse of exponential functions.
- Exponential Form: Logarithmic functions can be rewritten in exponential form.
- Graph Behavior: Logarithmic functions pass through the point (1, 0) and approach infinity or negative infinity as the argument approaches 0 or infinity, respectively.
- Applications: Logarithmic functions are used in various fields for modeling exponential growth or decay, data analysis, and making predictions.
Converting between Logarithmic and Exponential Forms
Logarithmic and exponential functions are closely related and can be converted from one form to another. Understanding how to convert between logarithmic and exponential forms is an important skill in algebra and calculus.
Converting from exponential to logarithmic form:
To convert an exponential equation to logarithmic form, we need to identify the base and exponent in the exponential equation. The base becomes the base of the logarithm, and the exponent becomes the value that the logarithm is equal to. The result is a logarithmic equation in the form logb(x) = y, where b is the base, x is the value, and y is the exponent.
Converting from logarithmic to exponential form:
To convert a logarithmic equation to exponential form, we need to identify the base, value, and exponent in the logarithmic equation. The base becomes the base of the exponential equation, the value becomes the base raised to the exponent power, and the exponent becomes the result of the exponential equation. The result is an exponential equation in the form by = x, where b is the base, y is the exponent, and x is the value.
Converting between logarithmic and exponential forms allows us to solve equations and problems involving exponential and logarithmic functions. It is important to understand the relationship between these two forms and how to convert between them in order to manipulate and solve equations involving exponential and logarithmic functions.
Solving Logarithmic Equations

Logarithmic equations are equations that involve logarithms. They can be solved by using the properties of logarithms and algebraic techniques. In this section, we will discuss the steps to solve logarithmic equations.
Steps to Solve Logarithmic Equations:
- Step 1: Isolate the logarithmic term on one side of the equation. If there are multiple logarithmic terms, combine them using the properties of logarithms.
- Step 2: Apply the inverse function of logarithm, which is exponentiation, to both sides of the equation to eliminate the logarithm.
- Step 3: Solve the resulting exponential equation for the variable.
- Step 4: Check the solutions by substituting them back into the original logarithmic equation. Make sure the solutions satisfy the equation.
It is important to note that logarithmic equations can sometimes have extraneous solutions, which are solutions that do not actually satisfy the original equation. Therefore, it is crucial to check the solutions obtained from solving the exponential equation in step 3.
In conclusion, solving logarithmic equations involves isolating the logarithmic term, applying exponentiation, and solving the resulting exponential equation. Always remember to check the solutions to ensure their validity.