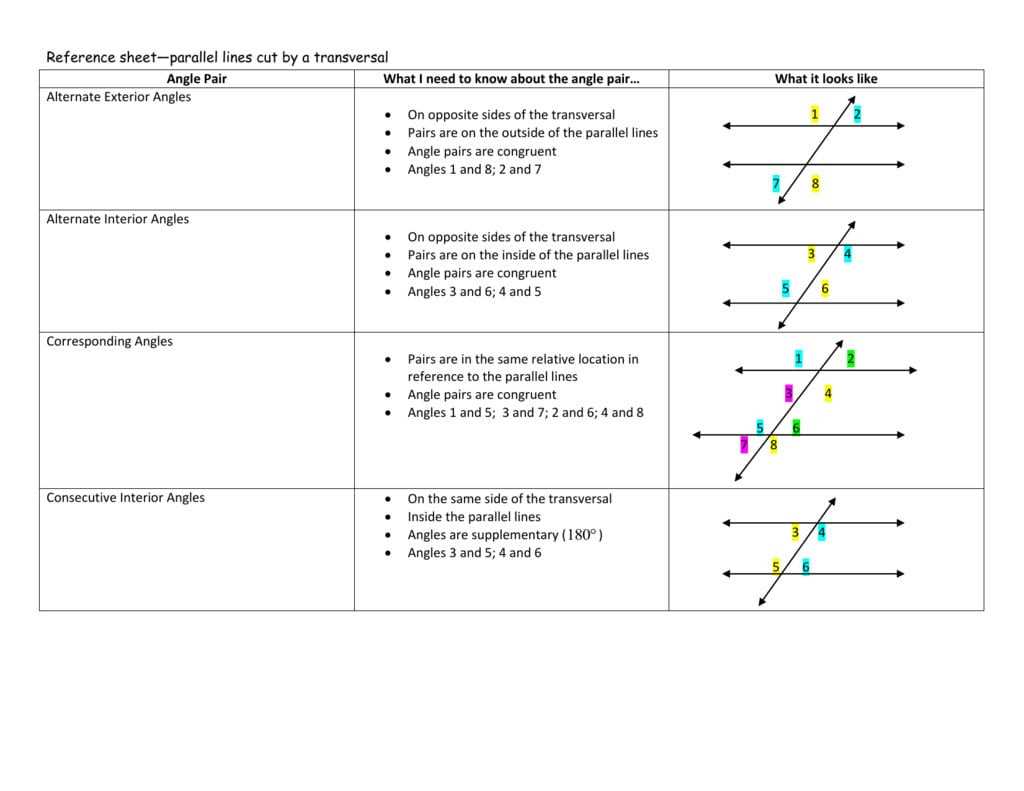
Understanding the concept of parallel lines and transversals is essential in geometry. When two lines are parallel, they never intersect, and they have the same slope. On the other hand, a transversal is a line that intersects two or more lines at different points.
In this article, we will explore the key concepts related to parallel lines and transversals and provide an answer key to help you check your understanding. We will cover topics such as corresponding angles, alternate interior angles, alternate exterior angles, consecutive interior angles, and supplementary angles.
To solve problems involving parallel lines and transversals, it is important to identify the different angles formed by the intersection. Corresponding angles are located in the same position on different lines and are congruent. Alternate interior angles are on opposite sides of the transversal and between the parallel lines. Alternate exterior angles, on the other hand, are also on opposite sides of the transversal but outside the parallel lines. Consecutive interior angles are adjacent angles on the same side of the transversal. Supplementary angles add up to 180 degrees.
Parallel Lines and Transversals Answer Key
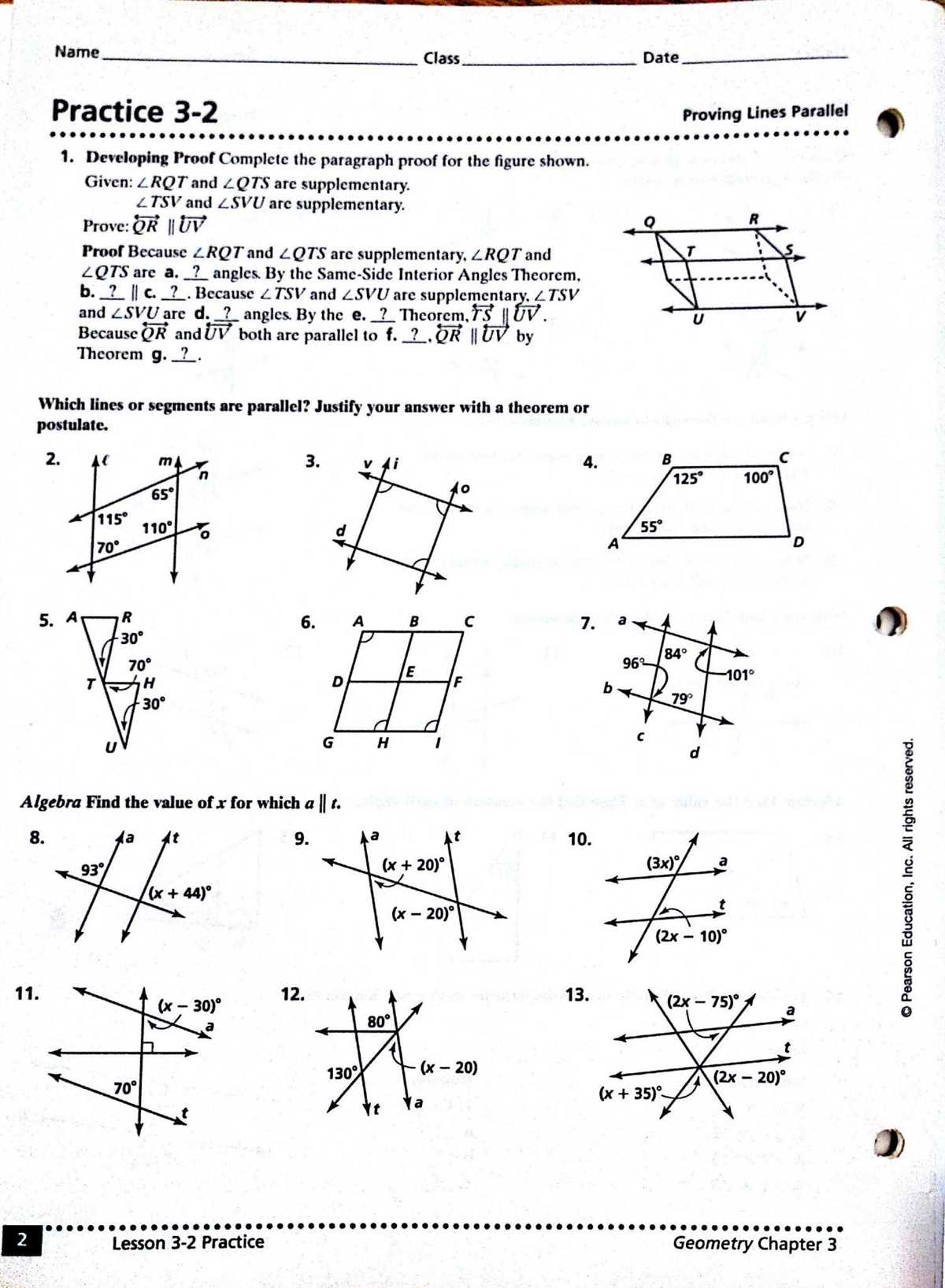
When studying geometry, one important concept to understand is parallel lines and transversals. Parallel lines are lines that never intersect, while transversals are lines that intersect two or more parallel lines. Exploring the relationships between these lines and angles formed by them is crucial in understanding geometric concepts and solving problems related to parallel lines and transversals.
One key aspect of studying parallel lines and transversals is identifying different angles formed by these lines. The answer key helps students determine the measures of various angles, such as corresponding angles, alternate interior angles, alternate exterior angles, and consecutive interior angles. By using this answer key, students can easily solve problems involving parallel lines and transversals by correctly identifying these angles and their properties.
The answer key also provides explanations and step-by-step solutions to different types of problems related to parallel lines and transversals. It helps students understand the properties and relationships of angles formed by parallel lines and transversals, allowing them to apply these concepts to solve more complex problems. The answer key serves as a valuable resource for students to check their answers, clarify their understanding, and learn from their mistakes.
- Corresponding angles: These are angles that are in the same position relative to the transversal and the parallel lines. They are equal in measure.
- Alternate interior angles: These are angles that are interior to the parallel lines and on opposite sides of the transversal. They are equal in measure.
- Alternate exterior angles: These are angles that are exterior to the parallel lines and on opposite sides of the transversal. They are equal in measure.
- Consecutive interior angles: These are angles that are interior to the parallel lines and on the same side of the transversal. They are supplementary, meaning their measures add up to 180 degrees.
In conclusion, the parallel lines and transversals answer key is an essential tool for students studying geometry. It helps them identify and understand the different angles formed by parallel lines and transversals, providing step-by-step solutions to problems and explanations of key concepts. By using the answer key, students can enhance their understanding of geometry and develop the skills necessary to solve problems involving parallel lines and transversals.
Understanding Parallel Lines and Transversals
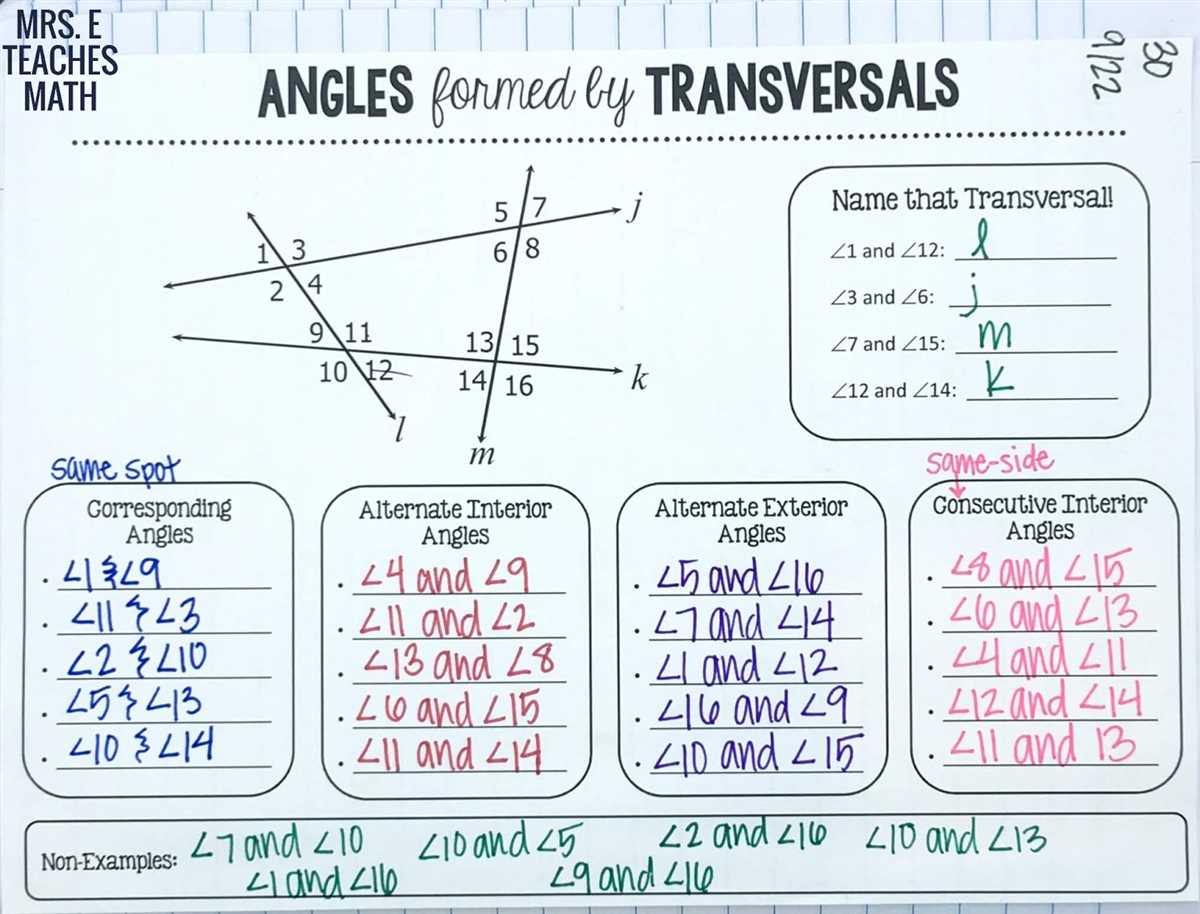
In geometry, parallel lines are lines that never intersect. They have the same slope, and no matter how far they are extended, they will never cross each other. Transversals, on the other hand, are lines that intersect two or more other lines.
When a transversal crosses two parallel lines, it creates several different angle relationships. These relationships can be classified into three main types: corresponding angles, alternate interior angles, and alternate exterior angles.
Corresponding angles are located in the same position of the intersected lines. For example, if we have line AB parallel to line CD, and transversal EF crosses both lines, angle 1 and angle 5 are corresponding angles because they are in the same position on the intersected lines.
Alternate interior angles are the angles formed on the inside of the intersected lines, but on opposite sides of the transversal. In the previous example, angle 2 and angle 8 are alternate interior angles.
Alternate exterior angles are the angles formed on the outside of the intersected lines, but on opposite sides of the transversal. In the previous example, angle 3 and angle 7 are alternate exterior angles.
Understanding these angle relationships is important in geometry as they allow us to prove various geometric theorems and solve geometric problems. By identifying and using the properties of parallel lines and transversals, we can determine the measure of angles and find missing angles in different geometric figures.
In summary, parallel lines and transversals create specific angle relationships, such as corresponding angles, alternate interior angles, and alternate exterior angles. By understanding these relationships, we can solve geometric problems and prove theorems in geometry.
Identifying Angle Relationships
When working with parallel lines and transversals, it is important to be able to identify and understand the different types of angle relationships that are formed. By knowing these angle relationships, we can determine the measures of angles and solve for unknown angles in a given diagram.
One important angle relationship is the corresponding angles. Corresponding angles are formed when a transversal intersects two parallel lines. These angles are in the same position relative to the transversal and the parallel lines. For example, if a transversal intersects two parallel lines and one pair of corresponding angles is labeled as ∠1 and ∠5, then we know that ∠1 is congruent to ∠5. Corresponding angles are important because they help us prove that lines are parallel or find the value of unknown angles.
Another angle relationship is the alternate interior angles. Alternate interior angles are formed when a transversal intersects two parallel lines and are located inside the parallel lines, on opposite sides of the transversal. These angles are congruent. For example, in a diagram where a transversal intersects two parallel lines and two pairs of alternate interior angles are labeled as ∠3 and ∠6, and ∠4 and ∠5, then we know that ∠3 is congruent to ∠6, and ∠4 is congruent to ∠5. Understanding alternate interior angles helps us prove that lines are parallel and find unknown angle measures.
By being able to identify and understand these angle relationships, we can apply them to various problems and solve for unknown angles. Practice and familiarity with these angle relationships will ensure our success in working with parallel lines and transversals.
Using Angle Relationships to Solve Problems

In geometry, angle relationships play a crucial role in solving various problems. By understanding the properties and rules governing angles, we can uncover hidden information and make connections between different parts of a geometric figure.
One of the fundamental angle relationships is that of complementary and supplementary angles. Complementary angles add up to 90 degrees, while supplementary angles add up to 180 degrees. These relationships can help us find missing angle measures or determine if two angles are related in a specific way.
Another important angle relationship is that of vertical angles. Vertical angles are opposite angles formed by the intersection of two lines. They have equal measures, which means that if we know the measure of one vertical angle, we can automatically determine the measure of its corresponding vertical angle.
Parallel lines and transversals also introduce a variety of angle relationships. For example, corresponding angles are congruent when a transversal intersects two parallel lines. Likewise, alternate interior angles and alternate exterior angles are congruent when a transversal intersects two parallel lines.
By identifying and applying these angle relationships, we can solve complex geometric problems. Whether it’s finding missing angle measures, proving congruence of angles, or establishing geometric properties, understanding angle relationships is essential for success in geometry.
Through practice and application, students can develop a deeper understanding of angle relationships and become skilled problem solvers in the realm of geometry.
Proving Lines are Parallel
When it comes to geometry, one of the important concepts to understand is parallel lines. Parallel lines are lines that are always the same distance apart and never intersect. There are several ways to prove that lines are parallel, and it often involves using the properties of angles and lines.
One common way to prove lines are parallel is by using the Alternate Interior Angles Theorem. This theorem states that if two parallel lines are cut by a transversal, then the alternate interior angles are congruent. To use this theorem to prove parallel lines, look for pairs of alternate interior angles that are congruent. If you can find such pairs, then you can conclude that the lines are parallel.
Another method to prove parallel lines is by using the Corresponding Angles Postulate. This postulate states that if two parallel lines are cut by a transversal, then the corresponding angles are congruent. To use this postulate to prove parallel lines, you need to find pairs of corresponding angles that are congruent. If you can find such pairs, then you can conclude that the lines are parallel.
Additionally, the Converse of the Corresponding Angles Postulate can also be used to prove parallel lines. This converse states that if two lines are cut by a transversal and the corresponding angles are congruent, then the lines are parallel. This means that if you can find pairs of corresponding angles that are congruent, you can conclude that the lines are parallel.
In summary, there are multiple ways to prove lines are parallel, including using the Alternate Interior Angles Theorem, the Corresponding Angles Postulate, and its converse. By identifying congruent angles within the given lines and transversals, you can determine whether the lines are parallel or not. These proofs rely on the properties of angles and lines, making them essential tools in geometry.
Applying Parallel Lines and Transversals to Real-world Situations
Parallel lines and transversals may seem like abstract mathematical concepts, but they have real-world applications that can help us understand and solve various problems. By understanding the properties and relationships between parallel lines and transversals, we can analyze and solve real-world situations more effectively.
One practical application of parallel lines and transversals is in architecture and construction. Architects and engineers often use parallel lines and transversals to design and construct buildings, bridges, and other structures. By utilizing parallel lines, they can ensure that different components of a structure, such as beams or walls, are properly aligned and supported. Transversals can also help determine the angles at which different components intersect, facilitating the construction process.
Parallel lines and transversals are also relevant in transportation and urban planning. Traffic lights and road markings are designed using parallel lines and transversals to ensure safe and efficient traffic flow. By understanding the concepts of parallel lines and transversals, traffic engineers can optimize lane configurations and intersections to minimize congestion and accidents.
Parallel lines and transversals can also be applied in the field of geometry. They provide a basis for understanding and solving problems related to angles, triangles, and polygons. For instance, the properties of angles formed by parallel lines and transversals help in the calculation of interior and exterior angles of polygons, which is essential in fields like surveying and mapmaking.
In conclusion, parallel lines and transversals have practical applications in various fields, such as architecture, construction, transportation, and geometry. By understanding and utilizing these concepts, we can solve real-world problems more effectively and efficiently. Whether it is designing structures, planning traffic flow, or calculating angles, parallel lines and transversals play a crucial role in improving our understanding of the physical world and helping us make informed decisions.