
Geometry is a branch of mathematics that deals with the properties, measurement, and relationships of points, lines, angles, and figures. It plays a crucial role in various fields, including architecture, engineering, and physics. Chapter 12 is a particularly important section in geometry, as it focuses on key concepts such as circles, arcs, and angles.
In this article, we will provide detailed answers to the questions and exercises presented in Chapter 12 of your geometry textbook. Our goal is to help you better understand the concepts covered and enhance your problem-solving skills. Whether you’re a student preparing for a test or an educator looking for additional resources, this guide will serve as a valuable reference.
Throughout this article, we will cover topics such as the properties of circles, the measurements of angles in a circle, and the relationship between arc lengths and angles. We will provide step-by-step explanations and examples to illustrate each concept, ensuring that you grasp the fundamentals and are able to apply them effectively.
Chapter 12 Geometry Answers
In Chapter 12 of our geometry textbook, we explore various concepts and problems related to geometric shapes and their properties. This chapter focuses on important topics such as angles, triangles, polygons, circles, and transformations. Throughout the chapter, students are introduced to theorems, definitions, and formulas that are essential for understanding and solving geometry problems.
One of the key concepts covered in this chapter is the properties of angles. Students learn about different types of angles, including acute, obtuse, right, and straight angles. They also learn about complementary and supplementary angles, as well as vertical angles. By understanding these properties, students are able to identify and solve problems involving angles in various geometric figures.
Another important topic in Chapter 12 is the properties of triangles. Students learn about different types of triangles, such as equilateral, isosceles, and scalene triangles. They also learn about the properties of interior and exterior angles of triangles, the Pythagorean theorem, and the triangle inequality theorem. These concepts are crucial for solving problems involving triangles, whether it’s determining side lengths, angles, or congruency.
Additionally, Chapter 12 covers polygons, which are closed figures formed by straight line segments. Students learn about different types of polygons, including quadrilaterals, pentagons, hexagons, and octagons. They learn about the properties of regular polygons, as well as formulas for finding the interior and exterior angles of polygons. By understanding these concepts, students can solve problems involving the sides, angles, and perimeter of polygons.
Lastly, Chapter 12 introduces students to the concept of circles. They learn about the parts of a circle, including the radius, diameter, chord, and circumference. They also learn about central angles, inscribed angles, and theorems related to circles, such as the angle at the center theorem and the angles in a semicircle theorem. These concepts are essential for solving problems involving circles, whether it’s finding the area, circumference, or arc length.
In conclusion, Chapter 12 of our geometry textbook provides students with a comprehensive understanding of various geometrical concepts and their applications. By studying and practicing the concepts covered in this chapter, students will be able to solve a wide range of geometry problems and further their understanding of the subject.
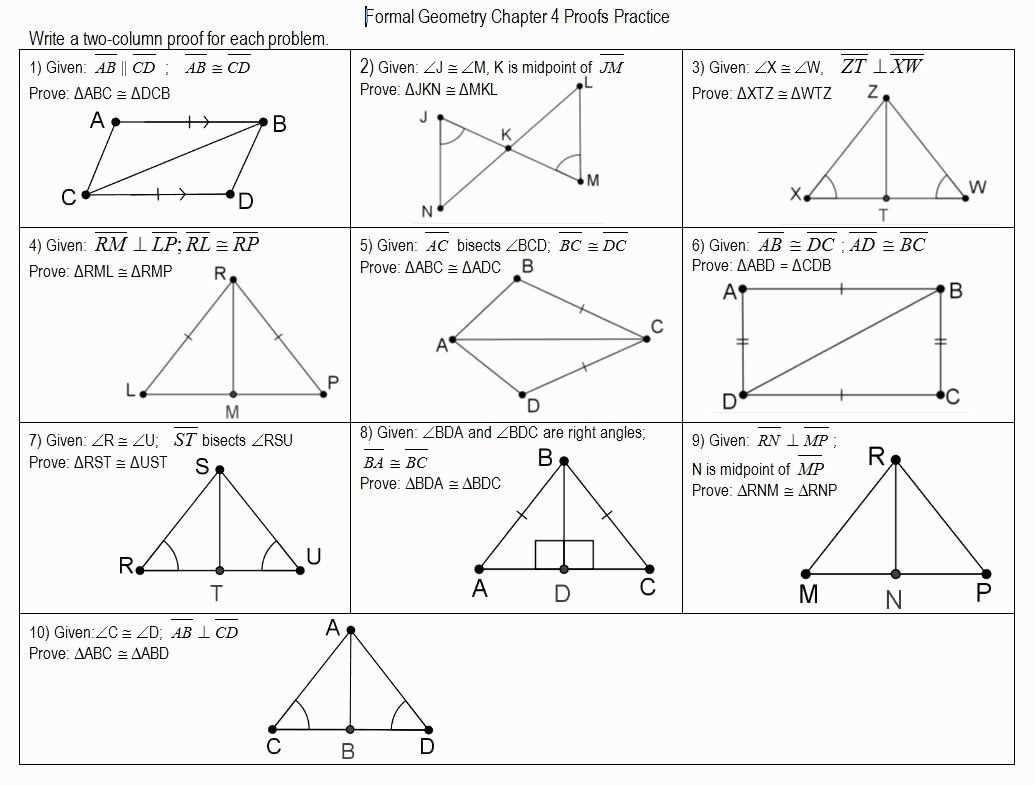
Exploring the Concept of Geometry
Geometry is a fascinating branch of mathematics that deals with the study of shapes, sizes, and properties of figures in space. It explores the relationships between points, lines, angles, and surfaces, and provides a framework for understanding the structures and patterns in the physical world.
One of the fundamental concepts in geometry is that of a point. A point is a location that has no size or dimension, and it serves as the building block for constructing lines, angles, and shapes. From points, we can define lines, which are straight paths that extend infinitely in both directions. Lines are characterized by their properties, such as being parallel, intersecting, or perpendicular to each other.
Angles are another important concept in geometry. They are formed by two intersecting lines or line segments and are measured in degrees. Angles can be classified into different types, such as acute, right, obtuse, or straight, based on their degrees of measurement. Understanding angles helps us analyze shapes, determine their symmetry, and solve various geometric problems.
In geometry, shapes play a crucial role. Shapes can be classified into two-dimensional (2D) and three-dimensional (3D) forms. 2D shapes, such as triangles, circles, and squares, are flat and have only length and width. 3D shapes, on the other hand, have an additional dimension of depth, such as cubes, spheres, and pyramids. Exploring the properties, formulas, and relationships of these shapes helps us calculate areas, volumes, and identify geometric characteristics.
In conclusion, geometry is an exciting field that enables us to understand and analyze the world around us. By exploring the concepts of points, lines, angles, and shapes, we can gain insights into the properties and relationships that exist in our physical environment. Geometry is not only relevant in mathematics but also has practical applications in various disciplines such as architecture, engineering, physics, and computer graphics.
Understanding the different types of angles
An angle is a geometric figure formed by two rays that share a common endpoint. Understanding the different types of angles is crucial in geometry as it allows us to classify and analyze shapes and their properties.
1. Acute angle: An acute angle is any angle that measures less than 90 degrees. It is smaller than a right angle and larger than a straight angle. For example, a triangle with three acute angles is called an acute triangle.
2. Right angle: A right angle is an angle that measures exactly 90 degrees. It forms the basis for many geometric constructions and is often used as a reference angle when measuring or drawing other angles. In a square or rectangle, all four interior angles are right angles.
3. Obtuse angle: An obtuse angle is any angle that measures greater than 90 degrees but less than 180 degrees. It is larger than a right angle and smaller than a straight angle. For example, in a triangle, one angle measures more than 90 degrees, it is considered an obtuse triangle.
4. Straight angle: A straight angle is an angle that measures exactly 180 degrees. It forms a straight line and is the largest possible angle. In a line segment, all four angles are straight angles.
5. Reflex angle: A reflex angle is any angle that measures greater than 180 degrees but less than 360 degrees. It is larger than a straight angle and smaller than a full rotation. Reflex angles are often found in polygonal shapes with more than three sides.
Solving problems involving parallel lines and transversals
A transversal is a line that intersects two or more parallel lines. When working with parallel lines and transversals, there are several key concepts to understand and apply in order to solve problems.
One important concept is the relationship between corresponding angles. When a transversal intersects two parallel lines, the corresponding angles formed are congruent. This means that if two angles are corresponding, they have the same measure. By identifying corresponding angles, you can use them to find missing angle measurements and solve problems involving parallel lines and transversals.
Another important concept is the relationship between alternate interior angles. When a transversal intersects two parallel lines, the alternate interior angles formed are congruent. This means that if two angles are alternate interior angles, they have the same measure. By identifying alternate interior angles, you can use them to find missing angle measurements and solve problems involving parallel lines and transversals.
In addition to corresponding angles and alternate interior angles, there are also relationships between alternate exterior angles and consecutive interior angles. By understanding these relationships and using them to identify congruent angles, you can solve problems involving parallel lines and transversals.
Applying the Pythagorean Theorem to solve for missing side lengths
The Pythagorean Theorem is a fundamental concept in geometry that allows us to relate the side lengths of a right triangle. It states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
When solving for missing side lengths using the Pythagorean Theorem, we start by identifying the right triangle and labeling its sides. We then apply the formula: a^2 + b^2 = c^2, where a and b are the lengths of the legs of the right triangle, and c is the length of the hypotenuse.
To solve for a missing side, we rearrange the formula to isolate the unknown variable. For example, if we are trying to find the length of one of the legs (a), we would rearrange the formula as: a^2 = c^2 – b^2. Then, we take the square root of both sides to find the value of a.
It’s important to note that when applying the Pythagorean Theorem, we must make sure we are working with a right triangle. If we are given a triangle that is not right-angled, the theorem cannot be used.
Overall, the Pythagorean Theorem is a powerful tool that allows us to solve for missing side lengths in right triangles. By understanding and applying this theorem, we can confidently tackle geometry problems involving right triangles and further our understanding of the relationships between their side lengths.
Exploring the properties of triangles and quadrilaterals
In the study of geometry, triangles and quadrilaterals are two fundamental types of polygons that have distinct properties and characteristics. By understanding these properties, we can gain a deeper insight into the relationships and properties of these shapes, and how they can be applied in various geometric problems and real-world situations.
Triangles, for example, are polygons with three sides and three angles. One important property of triangles is the sum of their interior angles, which always adds up to 180 degrees. This property allows us to calculate missing angles in a triangle when we have information about the other angles. Additionally, triangles can be classified based on the lengths of their sides and the measures of their angles, leading to different types such as equilateral, isosceles, and scalene triangles.
Properties of Triangles:
- The sum of the interior angles is always 180 degrees.
- The sum of the lengths of any two sides is always greater than the length of the third side (Triangle Inequality Theorem).
- There are different types of triangles, including equilateral, isosceles, and scalene triangles.
- The lengths of the sides and the measures of the angles can be used to classify triangles.
Quadrilaterals, on the other hand, are polygons with four sides and four angles. Unlike triangles, the sum of the interior angles of a quadrilateral is always 360 degrees. Additionally, quadrilaterals can have different properties based on the lengths of their sides, the measures of their angles, and the relationships between their sides and angles. Some common types of quadrilaterals include rectangles, parallelograms, squares, and trapezoids.
Properties of Quadrilaterals:
- The sum of the interior angles is always 360 degrees.
- Quadrilaterals can have different properties based on the lengths of their sides, the measures of their angles, and the relationships between their sides and angles.
- Some common types of quadrilaterals include rectangles, parallelograms, squares, and trapezoids.
By exploring and understanding the properties of triangles and quadrilaterals, we can not only solve geometric problems but also apply this knowledge to various fields such as architecture, engineering, and design. These shapes play a crucial role in the study of geometry and provide a foundation for more advanced concepts in mathematics.
Applying formulas to calculate the area and perimeter of different shapes
When dealing with various shapes in geometry, it is important to be able to calculate their area and perimeter accurately. By applying the appropriate formulas, we can determine these values and gain a better understanding of the shape’s properties.
For example, when working with rectangles, the formula for finding the area is length times width. By multiplying these two values together, we can determine the amount of space within the rectangle. Additionally, the perimeter of a rectangle can be calculated by adding up all four sides. This can provide us with the total length of the outer boundary of the shape.
Similarly, when working with circles, the formula for finding the area is pi times the radius squared. By substituting the value of the radius into this formula, we can determine the amount of space enclosed by the circle. The perimeter of a circle is commonly referred to as its circumference and can be calculated using the formula 2 times pi times the radius. This provides us with the length of the outer edge of the circle.
Other shapes, such as triangles and parallelograms, have their own specific formulas for calculating area and perimeter. For triangles, the area can be found using the formula one-half times base times height, while the perimeter can be found by adding up the lengths of all three sides. Parallelograms have similar formulas, with area being base times height and perimeter being the sum of all four sides.
Overall, by applying the appropriate formulas, we can accurately calculate the area and perimeter of different shapes, allowing us to better understand their properties and make more informed calculations and decisions in the field of geometry.
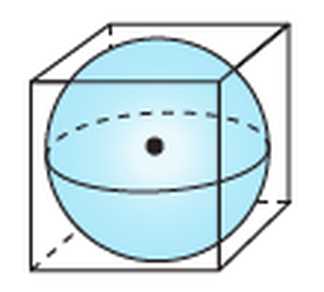
Exploring three-dimensional geometry and volume
In the study of geometry, three-dimensional shapes are an essential concept to comprehend. These shapes, also known as 3D shapes, have length, width, and height, adding another dimension to the traditional two-dimensional shapes found in plane geometry. By understanding the properties and characteristics of 3D shapes, mathematicians and scientists can analyze and calculate their volumes, surface areas, and other properties.
There are several types of 3D shapes, including prisms, pyramids, cylinders, cones, and spheres. These shapes can have different numbers of faces, edges, and vertices, leading to varied structures and characteristics. For example, a prism has two identical bases connected by multiple rectangular faces, while a cone has one circular base and a pointed vertex.
The concept of volume is crucial when studying three-dimensional geometry. Volume refers to the amount of space enclosed by a 3D shape and is measured in cubic units. By calculating the volume of a shape, mathematicians can quantify its capacity or amount of content it can hold. The formulas to compute volume differ depending on the shape, such as the formula V = Bh for prisms and V = 1/3πr^2h for cones.
Exploring three-dimensional geometry and volume allows us to understand and analyze objects in the real world. From calculating the volume of a water tank to determining the capacity of a pill bottle, three-dimensional geometry plays a significant role in various fields, including architecture, engineering, and physics. By mastering these concepts, we can better comprehend and manipulate the spatial dimensions around us.