
Polynomial functions are an important topic in Algebra 2, as they provide a foundation for understanding more complex equations and graphs. Unit 3 of Algebra 2 focuses on polynomial functions and explores their properties and characteristics.
To effectively study and practice polynomial functions, it is essential to have access to the answer key for assignments and assessments. The answer key serves as a guide to check for correctness and provides a way to understand any mistakes or misconceptions.
With the Algebra 2 Unit 3 Polynomial Functions Answer Key, students can review their work and compare their answers to the correct solutions. This helps them identify any errors or areas where they need to improve their understanding.
Additionally, the answer key allows teachers to provide timely feedback to their students. By using the answer key, teachers can see common mistakes and misconceptions that many students may have and address them in class or during one-on-one sessions.
Algebra 2 Unit 3 Polynomial Functions Answer Key
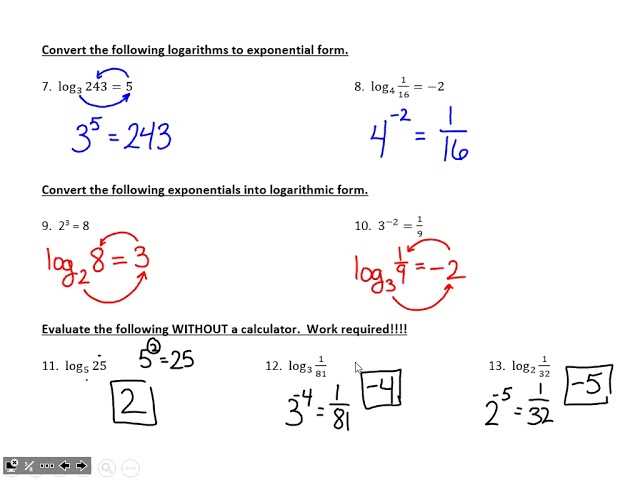
In Algebra 2, Unit 3 covers polynomial functions, which are algebraic expressions that involve variables raised to whole number powers. The answer key for this unit provides solutions to exercises and problems related to polynomial functions.
The answer key includes step-by-step explanations and calculations, allowing students to check their work and understand the process of solving polynomial functions. It also helps teachers to assess the accuracy of student responses and provide feedback.
The answer key covers various topics within polynomial functions, such as polynomial operations, factoring, finding zeros and roots, long division, synthetic division, and solving equations. It includes examples and practice problems that cover different difficulty levels, ensuring a comprehensive understanding of the subject.
By using the answer key, students can verify their solutions, identify any mistakes, and learn from them. It allows them to practice the skills and techniques necessary to master polynomial functions, leading to improved performance in exams and assignments.
The Algebra 2 Unit 3 Polynomial Functions Answer Key is a valuable resource that supports both students and teachers in navigating the complex world of polynomial functions.
Section 1: Defining Polynomial Functions
A polynomial function is a mathematical function that consists of one or more terms, each of which is a monomial with a variable raised to a non-negative integer exponent. The general form of a polynomial function is:
f(x) = anxn + an-1xn-1 + … + a1x + a0
Where f(x) represents the polynomial function, a is a constant coefficient, x is the variable, and n is a non-negative integer representing the degree of the polynomial.
A polynomial function can have multiple terms, and each term can have a different degree. The highest degree term in a polynomial function determines its overall degree. For example, if the highest degree term has a degree of 3, the polynomial function is said to have a degree of 3.
Polynomial functions are used to model and solve a wide range of real-world problems in areas such as physics, engineering, economics, and finance. They provide a flexible and powerful tool for representing relationships between variables and making predictions or calculations based on these relationships.
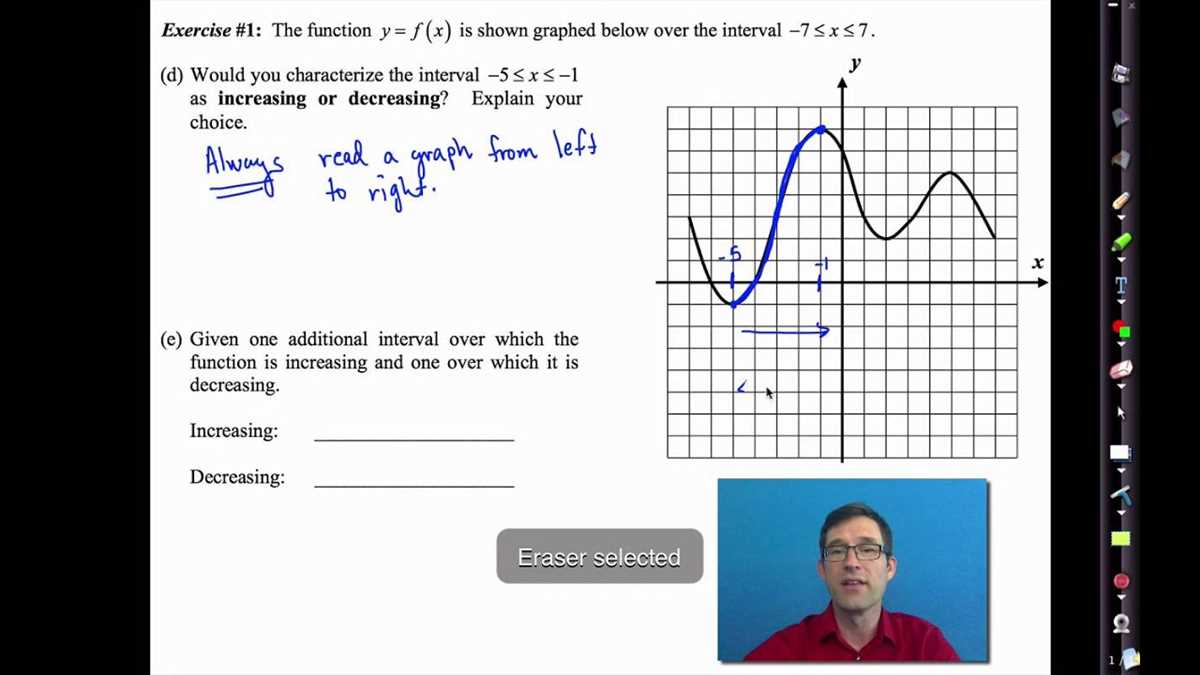
Section 2: Graphing Polynomial Functions
Graphing polynomial functions is an important skill to develop in Algebra 2. By understanding how to graph these functions, we can study their behavior, identify key features, and solve real-world problems. In this section, we will explore different methods and strategies for graphing polynomial functions.
1. Finding the x-intercepts: One way to start graphing a polynomial function is to find its x-intercepts or zeros. These are the values of x for which the function equals zero. To find the x-intercepts, we can set the polynomial equation equal to zero and solve for x. The x-intercepts will give us important information about the shape and behavior of the graph.
2. Determining the end behavior: Another important aspect of graphing polynomial functions is determining their end behavior. End behavior refers to how the function behaves as x approaches positive or negative infinity. By looking at the leading coefficient and the degree of the polynomial function, we can determine whether the graph will increase or decrease without bound on either side.
3. Graph transformations: Polynomial functions can also undergo transformations that change their shape and position on the coordinate plane. These transformations include vertical shifts, horizontal shifts, reflections, and stretching or shrinking. By identifying these transformations and applying them to the parent function, we can accurately graph polynomial functions.
- Vertical shifts: A vertical shift moves the graph up or down without changing its shape. The equation of a vertically shifted polynomial function is given by f(x) = g(x) + k, where g(x) is the parent function and k is the vertical shift.
- Horizontal shifts: A horizontal shift moves the graph left or right without changing its shape. The equation of a horizontally shifted polynomial function is given by f(x) = g(x – h), where g(x) is the parent function and h is the horizontal shift.
- Reflections: A reflection flips the graph over an axis. The equation of a reflected polynomial function is given by f(x) = -g(x), where g(x) is the parent function.
- Stretching and shrinking: A stretching or shrinking changes the steepness or width of the graph. The equation of a stretched or shrunk polynomial function is given by f(x) = a * g(x), where g(x) is the parent function and a is a positive constant.
By using these strategies and techniques, we can effectively graph polynomial functions and gain insights into their behavior and properties.
Section 3: Factoring Polynomial Functions
In algebra, factoring is an important process that involves breaking down a polynomial function into simpler forms. This section focuses on the concept of factoring polynomial functions and understanding how to factor them.
One key concept in factoring polynomial functions is the notion of finding the greatest common factor (GCF) of the terms in the function. By identifying the GCF, we can factor out common factors from each term and simplify the expression. This helps in reducing the complexity of the polynomial function and makes it easier to work with.
In addition to GCF, another important factorization method is factoring by grouping. This method involves grouping terms in a polynomial function and finding common factors within each group. By factoring out these common factors, we can simplify the expression further.
Factoring polynomial functions allows us to identify the roots or zeros of the function, which represent the values of x that make the function equal to zero. These roots can help us analyze the behavior of the function and find important points such as intercepts or turning points.
Overall, factoring polynomial functions is an essential skill in algebra that helps us manipulate and understand complex expressions. It allows us to simplify the functions, analyze their behavior, and solve equations involving polynomials. Mastery of factoring techniques is crucial for success in advanced algebra and calculus.
Section 4: Solving Polynomial Equations
In this section, we covered various methods to solve polynomial equations. We learned about factoring, where we break down a polynomial into its factors and set each factor equal to zero to find the solutions. We also discussed the Zero Product Property, which states that if the product of two factors is zero, then at least one of the factors must be zero.
Additionally, we explored the Rational Zero Theorem, which helps us find potential rational solutions by considering the factors of the constant term and the leading coefficient. We can then test these potential solutions using synthetic division to determine if they are actual solutions.
We also discussed the Fundamental Theorem of Algebra, which states that every polynomial equation of degree n has exactly n complex solutions, counting multiplicities. This theorem helps us understand the number and nature of solutions for a polynomial equation, whether they are real or complex.
In summary, solving polynomial equations involves various techniques such as factoring, using the Zero Product Property, applying the Rational Zero Theorem, and considering the Fundamental Theorem of Algebra. These methods allow us to find the solutions to polynomial equations, which are crucial in understanding the behavior and roots of polynomial functions.