
In lesson 10.6, we will be exploring the concept of the volume of a sphere. A sphere is a three-dimensional object that is perfectly round in shape. It is formed by taking all the points in space that are a fixed distance from a central point. The volume of a sphere is the amount of space inside the sphere. In this lesson, we will learn how to calculate the volume of a sphere using the formula V = (4/3)πr^3.
To calculate the volume of a sphere, we need to know the radius of the sphere. The radius is the distance from the central point of the sphere to any point on its surface. Once we have the radius, we can plug it into the formula V = (4/3)πr^3 to find the volume. The value of π (pi) is a mathematical constant that represents the ratio of the circumference of a circle to its diameter. It is approximately equal to 3.14159, but can be approximated as 3.14 for simplicity.
By using the formula V = (4/3)πr^3, we can easily find the volume of a sphere for any given radius. The volume is expressed in cubic units, such as cubic inches or cubic centimeters. Understanding how to calculate the volume of a sphere is useful in various applications such as engineering, architecture, and physics. It allows us to determine the amount of space an object takes up, which can be helpful when designing structures or predicting the behavior of physical systems.
Lesson 10.6 Volume of a Sphere Answers
In this lesson, we will explore the concept of volume in the context of a sphere. A sphere is a three-dimensional object with all points equidistant from its center. The volume of a sphere can be calculated using the formula V = 4/3πr^3, where V represents the volume and r represents the radius of the sphere.
To find the volume of a sphere using this formula, we first need to know the radius of the sphere. Once we have the radius, we can plug it into the formula and calculate the volume. It is important to remember that the radius must be in the same units as the volume. For example, if the radius is given in centimeters, the volume will be in cubic centimeters.
This formula can be applied to real-life situations where the volume of a sphere needs to be calculated. For example, if you are a scientist studying the properties of a spherical cell, knowing its volume can help you determine various characteristics, such as its density or surface area. Additionally, understanding the volume of a sphere can be useful in fields like engineering or architecture, where spherical objects are commonly encountered.
It is important to note that the volume of a sphere is always positive, as it represents the amount of space enclosed by the object. If the radius of the sphere is zero, the volume will also be zero, as there is no space enclosed. Similarly, if the radius is negative or imaginary, the volume will not be defined, as it does not make sense in the context of a physical object.
To summarize, the volume of a sphere can be calculated using the formula V = 4/3πr^3. This formula is applicable to various real-life scenarios and can be used to determine the amount of space enclosed by a spherical object. It is important to have the radius in the same units as the volume and to remember that the volume is always positive.
What is the formula for calculating the volume of a sphere?
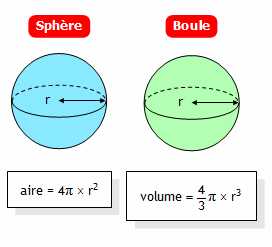
A sphere is a three-dimensional geometric shape that is perfectly symmetrical, meaning it looks the same from any angle. To calculate the volume of a sphere, we use a specific formula. The formula for calculating the volume of a sphere is:
V = (4/3) * π * r³
Where V represents the volume, π (pi) is a mathematical constant approximately equal to 3.14159, and r is the radius of the sphere. The radius is the distance from the center of the sphere to any point on its surface.
The formula shows that to find the volume of a sphere, we need to cube the radius and then multiply it by four-thirds and pi. This formula is derived from mathematical principles and is widely used in various fields, including physics, engineering, and mathematics.
How can the formula be derived?

The formula for the volume of a sphere can be derived using calculus. To begin, let’s consider a sphere with radius r. We can imagine slicing the sphere into infinitesimally thin discs, just like we would slice a cake. Each disc will have a thickness of Δr, where Δ represents the change or infinitesimally small value.
Now, if we take one of these discs and expand it into a flat round shape, we will get a circular ring. The area of this ring can be found using the formula for the area of a circle, which is πr^2. The width or thickness of this ring will be Δr. Therefore, the volume of this ring can be calculated by multiplying the area of the ring by its thickness, giving us ΔV = πr^2Δr.
Now, to find the total volume of the sphere, we need to sum up the volumes of all these infinitesimally thin rings. This can be done by integrating ΔV over the entire range of the radius r, from 0 to R, where R is the radius of the sphere. The integral of πr^2Δr with respect to r will give us the volume of the sphere, which can be expressed as V = ∫(0 to R)πr^2dr.
Simplifying the integral, we get V = (4/3)πR^3 as the formula for the volume of a sphere. This derivation shows that the volume of a sphere is directly proportional to the cube of its radius, highlighting the three-dimensional nature of the shape.
Why is the formula for the volume of a sphere important?
The formula for the volume of a sphere is important because it allows us to calculate the amount of space occupied by a sphere. This is particularly useful in various fields such as physics, engineering, and architecture where understanding the volume of objects is crucial for design and calculations.
By knowing the volume of a sphere, we can determine how much material is needed to construct it, which is essential in manufacturing processes. It also helps in determining the capacity of containers or tanks that have a spherical shape. Whether it’s designing storage containers, building structures, or calculating the displacement of a solid object, the formula for the volume of a sphere enables accurate measurements and predictions.
- Physics: In physics, understanding the volume of a sphere is important for determining properties like density, pressure, and buoyancy. It helps in analyzing the behavior of fluids, predicting how they will interact with other objects, and calculating the forces acting on them.
- Engineering: In engineering, the volume of a sphere is crucial for designing objects with curved surfaces, such as tanks, pipes, and automotive parts. Engineers need to accurately calculate the volume to ensure optimal performance and proper integration within a larger system.
- Architecture: Architects often use the volume of a sphere as a starting point for designing structures with curved and spherical shapes. By understanding the volume, architects can create aesthetically pleasing and structurally sound buildings.
Overall, the formula for the volume of a sphere plays a fundamental role in various disciplines and real-world applications. It allows us to measure and quantify the space occupied by spheres, providing essential information for calculations, design, and analysis in diverse fields.
What are the units used to measure volume?
The volume of an object is a measure of the amount of space it occupies. It can be measured in various units depending on the nature of the object and the system of measurement being used. In general, volume is measured in cubic units.
In the metric system, commonly used units for measuring volume include cubic meters (m³), cubic centimeters (cm³), and liters (L). A cubic meter is equivalent to 1,000,000 cubic centimeters or 1,000 liters. Cubic centimeters are often used for smaller objects or precise measurements, while liters are commonly used for measuring larger quantities of liquids or gases.
In the imperial system, volume is typically measured in cubic inches (in³), cubic feet (ft³), or gallons (gal). One cubic foot is equal to 1,728 cubic inches or approximately 7.48 gallons. Gallons are commonly used for measuring liquids, especially in the United States, where they are used to measure fuel efficiency, quantities of liquids, and volumes of containers.
It’s important to note that volume can also be measured using non-standard units in certain contexts. For example, in cooking, teaspoons, tablespoons, and cups are commonly used to measure the volume of ingredients. These units are not standardized and may vary slightly in different regions.
In summary, the units used to measure volume depend on the system of measurement being used and the nature of the object being measured. In general, volume is measured in cubic units such as cubic meters, cubic centimeters, cubic inches, cubic feet, liters, and gallons.
Can the volume of a sphere be negative?
No, the volume of a sphere cannot be negative.
A sphere is a three-dimensional object with no flat sides or edges. It is defined as the set of all points in space that are equidistant from a given point, called the center. The volume of a sphere is the amount of space it occupies.
The formula to calculate the volume of a sphere is: V = (4/3)πr³, where V is the volume and r is the radius. The radius, which is the distance between the center of the sphere and any point on its surface, is always a positive value.
Since both π (pi) and r³ are positive values, the result of the calculation will also be positive. Therefore, the volume of a sphere is always a positive number, and it cannot be negative.
How does the radius of a sphere affect its volume?
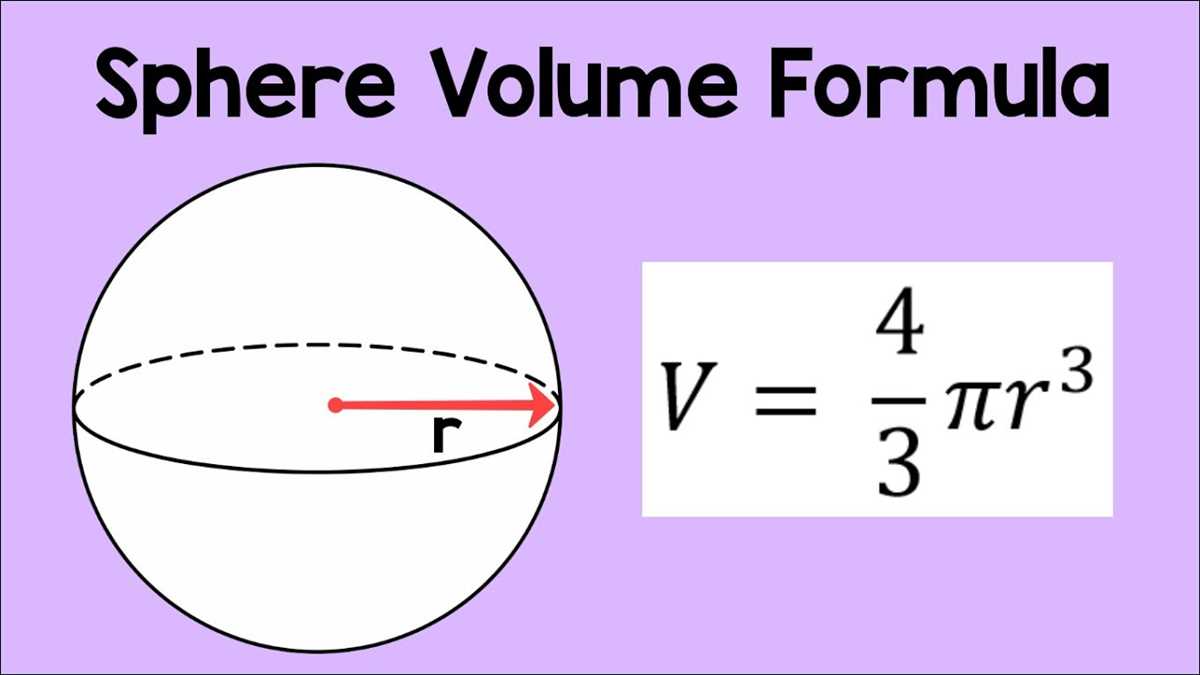
The volume of a sphere is directly influenced by its radius. The radius of a sphere is the distance from its center to any point on its surface. As the radius of a sphere increases, so does its volume. This means that larger spheres have a greater volume than smaller spheres, assuming all other factors remain constant.
This relationship can be explained by the formula used to calculate the volume of a sphere, which is V = (4/3)πr³. In this formula, “V” represents the volume of the sphere and “r” represents its radius. The radius is raised to the power of 3, which means that even a small increase in the radius can lead to a significant increase in the volume.
For example, let’s consider two spheres with radii of 2 units and 4 units. Plugging these values into the volume formula, we find that the volume of the sphere with a radius of 2 units is approximately 33.51 cubic units, while the volume of the sphere with a radius of 4 units is approximately 268.08 cubic units. We can see that doubling the radius results in an eightfold increase in volume.
Therefore, it is clear that the radius of a sphere has a direct impact on its volume. As the radius increases, the volume also increases exponentially. This relationship is important to understand when working with spheres in various mathematical and real-world scenarios, such as calculating the volume of a water tank or the size of a planet.
Real-life applications of calculating the volume of a sphere
The volume of a sphere is a mathematical concept that has numerous real-life applications. Here are a few examples:
1. Architecture and construction: Calculating the volume of a sphere is important in architectural and construction design. Architects and engineers use the volume of a sphere when designing domes, arches, and other curved structures. By accurately calculating the volume, they can ensure that the structure can withstand the required load and have the necessary space for its intended purpose.
2. Tank volume calculation: Industries that store liquids, such as oil, water, and chemicals, need to calculate the volume of their tanks. Many storage tanks have a spherical shape, as it allows for maximum volume with minimum surface area. By knowing the volume of a sphere, companies can determine the capacity of their tanks and plan accordingly for the storage and transportation of liquids.
3. Hydrology and environmental studies: Hydrologists and environmental scientists need to estimate the volume of bodies of water, such as lakes and ponds, for various research and management purposes. By measuring the diameter of the surface area of the water body, they can use the formula for the volume of a sphere to calculate its total volume. This information is crucial for understanding water resources, ecological studies, and pollution management.
4. Medicine and biology: The volume of a sphere is also relevant in the medical field, particularly in radiology and biology. Medical professionals use the volume of a sphere to calculate the size of tumors, cysts, and organs in the body. Surgical procedures, chemotherapy dosages, and other medical treatments often take into account the volume of a sphere to ensure accurate diagnosis and treatment.
5. Material science: Researchers and engineers working in material science use the volume of a sphere to understand and design properties of spherical particles and nanoparticles. By calculating the volume, they can determine the density and specific surface area, which are essential parameters for applications such as catalysis, drug delivery systems, and nanotechnology.
These are just a few examples of the real-life applications of calculating the volume of a sphere. Its mathematical concept is widely used across various industries and fields to solve practical problems and make accurate measurements.
Can the formula for calculating the volume of a sphere be applied to other three-dimensional shapes?
The formula for calculating the volume of a sphere, V = (4/3)πr³, is specific to the unique shape of a sphere. The volume of a sphere is determined by its radius, which is the distance from the center of the sphere to any point on its surface. This formula cannot be directly applied to other three-dimensional shapes because they have different geometrical properties.
However, there are formulas specific to different three-dimensional shapes that can be used to calculate their volumes. For example, the volume of a cube can be calculated using the formula V = s³, where s represents the length of one side of the cube. The volume of a cylinder can be calculated using the formula V = πr²h, where r represents the radius of the base and h represents the height of the cylinder.
Each three-dimensional shape has its own unique formula for calculating its volume based on its specific geometric properties. While the formula for the volume of a sphere cannot be directly applied to other shapes, understanding the concept of volume and the formulas for different shapes allows us to calculate the volume of various objects in the real world.