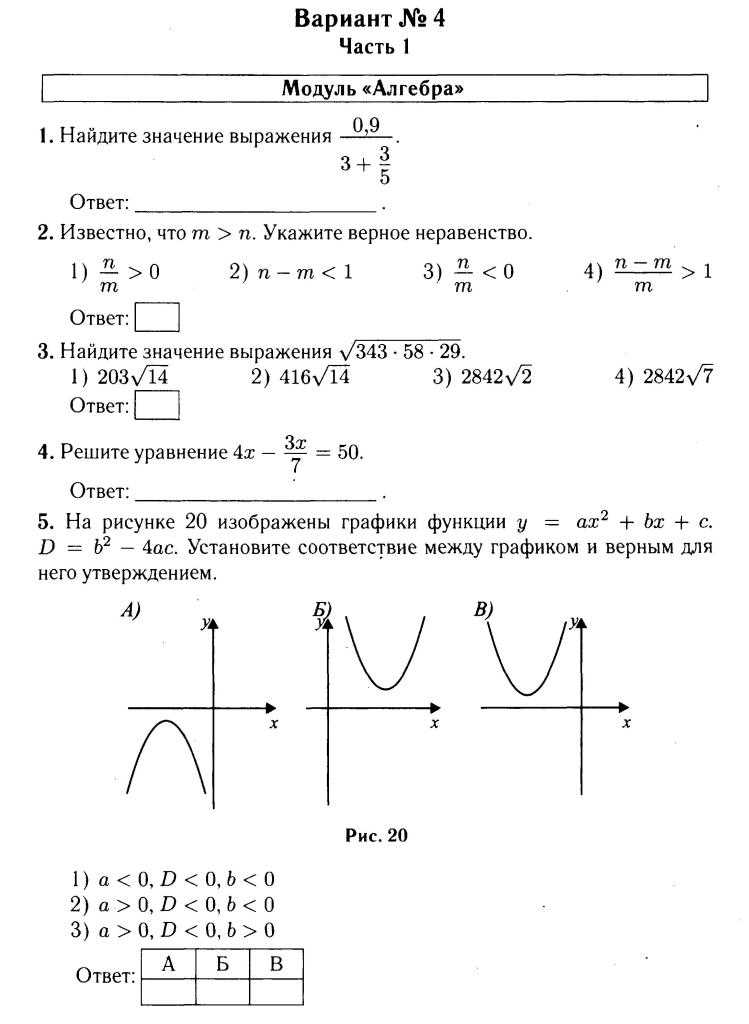
Algebra is a fundamental branch of mathematics that lays the foundation for numerous concepts and skills in various fields, including science, engineering, and economics. However, mastering algebra can be a challenging task for many students. That’s where Algebra Nation Section 9 comes in.
This crucial section delves deep into key algebraic principles, offering comprehensive explanations, interactive activities, and practice problems to help students solidify their understanding and proficiency. It covers topics such as solving linear equations, graphing inequalities, and working with systems of equations.
By providing answers to the Section 9 exercises, Algebra Nation gives students the opportunity to verify their solutions and identify areas where they may need additional support. Whether preparing for exams, reviewing concepts, or seeking extra practice, these answers serve as a valuable resource for students striving to improve their algebra skills and achieve academic success.
Overview of Algebra Nation Section 9 Answers
Section 9 of Algebra Nation covers the topic of linear equations, providing students with a comprehensive understanding of this fundamental concept in algebra. In this section, students will learn about the different forms of linear equations, including slope-intercept form, point-slope form, and standard form. They will also explore how to graph linear equations, determine the slope and y-intercept, and solve systems of linear equations.
To reinforce their understanding of linear equations, students can access the Algebra Nation Section 9 Answers, which provide step-by-step solutions to the practice problems and exercises in this section. The answers serve as a valuable resource for students to check their work and identify any mistakes they may have made. By reviewing the answers, students can gain insight into the correct approach to solving linear equations, allowing them to improve their problem-solving skills and build confidence in their algebraic abilities.
The Algebra Nation Section 9 Answers are presented in a clear and concise manner, making it easy for students to follow along and understand the solution process. Each answer is accompanied by a detailed explanation, offering insights into the underlying concepts and strategies used to arrive at the correct solution. This not only helps students determine the correct answer but also provides them with a deeper understanding of the mathematical principles involved in solving linear equations.
In addition to the step-by-step solutions, the Algebra Nation Section 9 Answers also include tips and tricks for solving linear equations more efficiently. These insights can help students streamline their problem-solving process and improve their overall mathematical proficiency. By utilizing these tips, students can save time and effort when solving linear equations, allowing them to tackle more complex problems and advance their algebraic skills.
In conclusion, the Algebra Nation Section 9 Answers play an integral role in guiding students through the concepts and techniques related to linear equations. By utilizing these answers, students can reinforce their understanding, identify and correct any mistakes, and improve their problem-solving abilities. This comprehensive resource helps students build a strong foundation in algebra and prepares them for more advanced mathematical concepts in the future.
The Importance of Understanding Algebra Nation Section 9
Algebra Nation Section 9 is a crucial component of the Algebra Nation curriculum, and it is important for students to understand its concepts and principles. This section focuses on various topics related to algebra, including linear functions, systems of equations, and inequalities. By mastering the concepts in this section, students can develop a strong foundation in algebra and build their problem-solving and critical thinking skills.
Linear functions play a vital role in algebra, as they provide a framework for understanding and analyzing relationships between variables. In Section 9, students learn how to graph linear functions and interpret the meaning of slope and y-intercept. This knowledge is crucial in various fields, such as economics, physics, and engineering, where linear relationships are frequently encountered.
Systems of equations are another important concept covered in Section 9. Understanding how to solve systems of equations allows students to find the intersection points of multiple lines or curves. This skill is essential in various real-life scenarios, such as solving optimization problems, analyzing market equilibrium, or designing strategies in game theory. The ability to solve systems of equations efficiently is an essential skill that students can apply in many fields.
Inequalities are also explored in Section 9. Inequalities provide a way to represent and analyze relationships that are not necessarily equal. Students learn how to graph and solve inequalities, which is essential in various areas, such as solving optimization problems, analyzing constraints in resource allocation, or understanding social and economic inequalities. Mastering the concepts of inequalities helps students develop their analytical skills and apply algebraic thinking in real-world contexts.
In conclusion, understanding Algebra Nation Section 9 is of paramount importance as it provides students with a strong foundation in algebraic concepts. The topics covered in this section, such as linear functions, systems of equations, and inequalities, have practical applications in various fields and help students develop problem-solving and critical thinking skills. By mastering the concepts in Section 9, students can gain a deeper understanding of algebra and be better equipped to tackle more advanced mathematical topics in the future.
Key Concepts Covered in Algebra Nation Section 9
The Algebra Nation Section 9 covers several key concepts that are essential for understanding algebra. These concepts include linear equations, slope-intercept form, point-slope form, and graphing linear equations.
One of the main topics in Section 9 is linear equations. Students will learn how to solve linear equations and understand the importance of finding the values that make an equation true. They will also learn how to represent linear equations in slope-intercept form, which is y = mx + b, where m represents the slope and b represents the y-intercept.
Another important concept covered in Section 9 is point-slope form. Students will learn how to use a given point on a line and the slope of the line to write the equation of the line in point-slope form. This form is represented as y – y1 = m(x – x1), where (x1, y1) represents the coordinates of the given point and m represents the slope.
Lastly, students will learn how to graph linear equations using the concepts of slope and y-intercept. They will explore how changing the values of m and b in the equation y = mx + b affects the graph of the line. They will also learn how to identify the slope and y-intercept from a given equation and use that information to graph the line.
Overall, Section 9 of Algebra Nation provides students with a solid foundation in linear equations and graphing. These concepts are fundamental in algebra and are necessary for solving a variety of mathematical problems.
Linear Equations and Inequalities

Linear equations and inequalities are fundamental concepts in algebra. They involve relationships between variables that are represented by straight lines on a graph. These equations and inequalities can be solved using various methods, such as substitution, elimination, or graphing.
A linear equation is an equation in which the highest power of the variable is 1. It represents a straight line on a graph. The goal is to find the value of the variable that satisfies the equation. For example, the equation 3x + 2 = 8 can be solved by isolating the variable x. By subtracting 2 from both sides of the equation and then dividing both sides by 3, we find that x = 2.
A linear inequality, on the other hand, represents a range of values that satisfy the inequality. For example, the inequality 2x + 3 < 7 represents all the values of x that make the expression 2x + 3 less than 7. We can solve this inequality by isolating x and finding that x < 2.
In algebra, linear equations and inequalities are used to model real-world problems, such as solving for unknown quantities or determining the feasibility of certain situations. They provide a way to represent and analyze relationships between variables and help to make predictions and solve problems.
Systems of Equations
In algebra, a system of equations refers to a set of two or more equations that are solved simultaneously. These equations usually have multiple variables, and the goal is to find the values of the variables that satisfy all of the equations. Solving systems of equations is an important skill in algebra, as it allows us to find the solutions to real-world problems that can be represented mathematically.
There are several methods for solving systems of equations, including graphing, substitution, and elimination. Graphing involves plotting the equations on a coordinate plane and finding the points of intersection. Substitution involves solving one equation for one variable and substituting that expression into the other equation. Elimination involves adding or subtracting the equations in order to eliminate one variable and then solving for the remaining variable.
Example:
Consider the following system of equations:
- Equation 1: 2x + 3y = 12
- Equation 2: 4x – 2y = 8
We can solve this system using the elimination method. Multiplying Equation 1 by 2 and Equation 2 by 3, we get:
- Equation 1: 4x + 6y = 24
- Equation 2: 12x – 6y = 24
Adding these two equations together, we eliminate the y variable:
- 16x = 48
Dividing both sides by 16, we find that x = 3. Substituting this value back into either of the original equations, we can solve for y. In this case, substituting x = 3 into Equation 1, we get:
- 2(3) + 3y = 12
- 6 + 3y = 12
- 3y = 6
- y = 2
Therefore, the solution to the system of equations is x = 3 and y = 2.
Summary
Systems of equations involve solving two or more equations simultaneously to find the values of the variables that satisfy all of the equations. There are several methods for solving these systems, such as graphing, substitution, and elimination. Each method has its advantages and may be more suitable for certain types of equations. Solving systems of equations is an essential skill in algebra, as it allows us to solve real-world problems using mathematical models.
Exponents and Exponential Functions
In algebra, exponents and exponential functions play a crucial role in solving various mathematical problems. An exponent is a number that represents how many times a base number is multiplied by itself. It is denoted by a superscript after the base number. For example, in the expression 2^3, the base number is 2, and the exponent is 3. This means that 2 is multiplied by itself 3 times, resulting in the value of 8.
Exponential functions, on the other hand, are functions where the variable is in the exponent. These functions have the general form f(x) = a^x, where a is the base number and x is the exponent. The value of the function depends on the values of a and x. Exponential functions can model various real-life situations, such as population growth, compound interest, and radioactive decay.
When working with exponents and exponential functions, it is important to understand the properties and rules that govern their behavior. These include the product rule, power rule, and quotient rule, which allow us to simplify and manipulate expressions involving exponents. Additionally, logarithms, which are the inverse operations of exponents, can also be used to solve exponential equations.
Exponents and exponential functions are fundamental concepts in algebra and have extensive applications in various fields, including finance, science, and engineering. Understanding these concepts can help us analyze and solve complex problems involving exponential growth or decay. By applying the rules and properties of exponents, we can simplify expressions and equations, making them easier to solve and interpret.
Tips and Strategies for Solving Problems in Algebra Nation Section 9

Solving problems in Algebra Nation Section 9 can be challenging, but with the right tips and strategies, you can succeed. Here are some helpful suggestions to tackle the problems in this section:
- Understand the problem: Before you start solving a problem, take the time to carefully read and understand what it is asking. Pay attention to any given information or conditions.
- Identify the key concepts: Once you understand the problem, identify the key concepts or equations that are relevant to solving it. This will help you focus your attention and make it easier to proceed.
- Use diagrams or tables: Sometimes, visualizing the problem with the help of diagrams or tables can make it easier to understand and work through. Consider creating a visual representation to help you organize the information and make connections.
- Break down the problem: If a problem seems too daunting, try breaking it down into smaller, more manageable parts. Solve each part separately and then bring them together to find the final solution.
- Practice using different methods: Algebra often has multiple methods or approaches to solving a problem. Practice using different methods to broaden your understanding and problem-solving skills. This will also help you find the most efficient approach for different types of problems.
Remember, practice is key when it comes to solving algebra problems. The more you practice, the more comfortable and confident you will become. Keep these tips and strategies in mind, and don’t be afraid to ask for help or seek additional resources when needed. With persistence and dedication, you can master Algebra Nation Section 9 and excel in your algebra studies.
Identifying the Type of Equation or Inequality

When solving algebraic equations or inequalities, it is important to first identify the type of equation or inequality that is being presented. This information will help guide our approach to finding a solution or determining the characteristics of the equation or inequality.
There are several types of equations and inequalities that we commonly encounter in algebra, including linear equations, quadratic equations, absolute value equations, and systems of equations. Each type has its own distinct characteristics and methods of solution.
Linear equations are equations in which the highest power of the variable is 1. They can be represented by a straight line on a coordinate plane and have solutions that form a straight line as well. Linear equations can often be solved by isolating the variable on one side of the equation.
Quadratic equations are equations in which the highest power of the variable is 2. They can be represented by a parabola on a coordinate plane and have solutions that form the shape of a parabola as well. Quadratic equations can be solved using different methods, such as factoring, completing the square, or using the quadratic formula.
Absolute value equations involve the absolute value of a variable. They can have multiple solutions and often involve solving for both the positive and negative values of the variable. Absolute value equations can be solved by setting up separate equations for the positive and negative cases and finding the solutions for each.
Systems of equations involve multiple equations with multiple variables. They represent a set of equations that must be satisfied simultaneously, meaning all the equations in the system must be true at the same time. Systems of equations can be solved using various methods, such as substitution, elimination, or graphing.
By identifying the type of equation or inequality we are dealing with, we can apply the appropriate techniques and strategies to find the solution or analyze the equation further. This understanding allows us to approach algebraic problems more effectively and confidently.