Algebra 2 is a critical subject for students looking to gain a strong foundation in mathematics. In Chapter 5, students are introduced to a range of advanced concepts that build upon their previous knowledge and challenge them to think critically and creatively.
One of the key topics covered in Chapter 5 is systems of linear equations. Students will learn how to solve these systems using a variety of methods, including substitution, elimination, and graphing. By exploring different approaches to solving systems, students can develop a deeper understanding of how mathematical concepts are interconnected and can be applied in real-world situations.
Another important focus of Chapter 5 is exponential and logarithmic functions. Students will learn how to analyze and graph these functions, as well as solve exponential and logarithmic equations. Understanding exponential and logarithmic functions is essential for a wide range of fields, including economics, biology, and engineering, making this chapter particularly relevant for students pursuing careers in these areas.
Furthermore, students will delve into the world of matrices and determinants in Chapter 5. They will learn about matrix operations, such as addition, subtraction, multiplication, and finding the inverse of a matrix. Additionally, students will explore how matrices can be used to solve systems of equations and represent transformations in two-dimensional space.
In this article, we will provide comprehensive answers to the exercises and problems presented in Algebra 2 Chapter 5. By reviewing these answers, students can solidify their understanding of the core concepts and improve their problem-solving skills. Whether preparing for an exam or seeking additional practice, these answers will serve as a valuable resource for students aiming to master the material covered in Chapter 5 of Algebra 2.
Chapter Summary
In Chapter 5 of Algebra 2, we explored various topics related to exponential and logarithmic functions. We began by reviewing the basic properties of exponents and how they can be used to simplify and solve equations. We then moved on to examining exponential functions and their key characteristics, such as growth and decay, domain and range, and asymptotes.
Next, we delved into logarithmic functions and their relationship to exponential functions. We learned about the properties of logarithms, including the product rule, quotient rule, and change of base formula. These properties allowed us to manipulate logarithmic expressions and solve logarithmic equations.
We also discussed the applications of exponential and logarithmic functions in real-world situations. We explored compound interest and continuous growth models, as well as exponential growth and decay in population and radioactive decay. These applications provided us with practical examples of how these functions can be used to model and analyze real-life phenomena.
To solidify our understanding of the material, we worked through numerous examples and practice problems. These exercises challenged us to apply our knowledge of exponential and logarithmic functions to various scenarios and develop our problem-solving skills.
Overall, Chapter 5 expanded our understanding of exponential and logarithmic functions and equipped us with the tools to solve a variety of problems involving these functions. By mastering the concepts and techniques covered in this chapter, we are better prepared to tackle more advanced topics in algebra and beyond.
Overview of Algebra 2 Chapter 5

In Algebra 2 Chapter 5, we will explore the topic of logarithms. Logarithms are an important concept in mathematics and have numerous applications in various fields such as science, engineering, and finance. This chapter will provide a comprehensive introduction to logarithmic functions, their properties, and their applications.
The chapter begins with an introduction to logarithms, where we will learn about the basic definition and notation of logarithms. We will explore the relationship between exponential and logarithmic functions and how they are inversely related to each other. This understanding is crucial as it forms the foundation for the rest of the chapter.
Next, we will dive deeper into logarithmic functions and their properties. We will learn about the basic properties of logarithms, including the product, quotient, and power rules. These properties will allow us to simplify and manipulate logarithmic expressions, making calculations and problem-solving easier.
In addition to properties, we will also explore the graphing of logarithmic functions. We will learn how to graph logarithmic equations and identify key features such as the domain, range, and asymptotes. Understanding the graphical representation of logarithmic functions will help us analyze and interpret real-world situations that involve exponential growth or decay.
Furthermore, this chapter will cover various applications of logarithms. We will learn how to solve exponential and logarithmic equations, as well as apply logarithmic functions to solve real-world problems. Examples of these applications include population growth, exponential decay, and financial investments.
By the end of Algebra 2 Chapter 5, you will have a solid understanding of logarithms and their applications. You will be able to solve logarithmic equations, interpret logarithmic graphs, and apply logarithmic functions to real-world scenarios. This knowledge will serve as a valuable tool in your mathematical journey and beyond.
Solving Linear Equations
Section 5.1 of Algebra 2 focuses on solving linear equations. In this section, we will learn how to find the values of variables that make an equation true. A linear equation is an equation in which the highest power of the variable is 1, and the equation represents a straight line when graphed.
To solve linear equations, we use various methods such as combining like terms, applying the distributive property, and isolating the variable. The goal is to manipulate the equation to isolate the variable on one side and the constants on the other side. This allows us to easily determine the value of the variable.
One method commonly used to solve linear equations is the addition and subtraction property of equality. This property states that if we add or subtract the same value from both sides of an equation, the equality is still maintained. By using this property, we can simplify the equation and solve for the variable.
Another method is the multiplication and division property of equality. This property states that if we multiply or divide both sides of an equation by the same non-zero value, the equality is still maintained. This allows us to manipulate the equation and find the value of the variable.
Solving linear equations is an essential skill in algebra as it helps us to analyze and solve real-world problems. By understanding the different methods and properties, we can confidently solve equations and find the solutions that make the equation true.
Step-by-Step Guide to Solving Linear Equations
Linear equations are fundamental concepts in algebra and are used to solve problems that involve unknown values. Here is a step-by-step guide to solving linear equations:
Step 1: Simplify Both Sides
The first step in solving a linear equation is to simplify both sides of the equation by combining like terms. This can be done by adding or subtracting terms on both sides of the equation to eliminate any unnecessary variables.
Step 2: Isolate the Variable

After simplifying both sides, the next step is to isolate the variable on one side of the equation. This can be done by adding or subtracting terms on both sides to move all terms containing the variable to one side and all constant terms to the other side of the equation.
Step 3: Solve for the Variable
Once the variable has been isolated, the next step is to solve for the variable by performing the necessary operations. This may involve dividing both sides of the equation by a coefficient, multiplying both sides by a common denominator, or applying other algebraic operations.
Step 4: Check the Solution
Finally, after obtaining a value for the variable, it is important to check the solution by substituting the value back into the original equation. If the equation holds true for the substituted value, then the solution is correct.
Step 5: Express the Solution

Express the solution as a single value or as a range of values, depending on the context of the problem. It is important to clearly state the solution and any restrictions, if applicable.
By following these step-by-step guidelines, solving linear equations becomes a systematic and efficient process. Practicing solving a variety of linear equations will help improve proficiency and confidence in algebraic problem-solving.
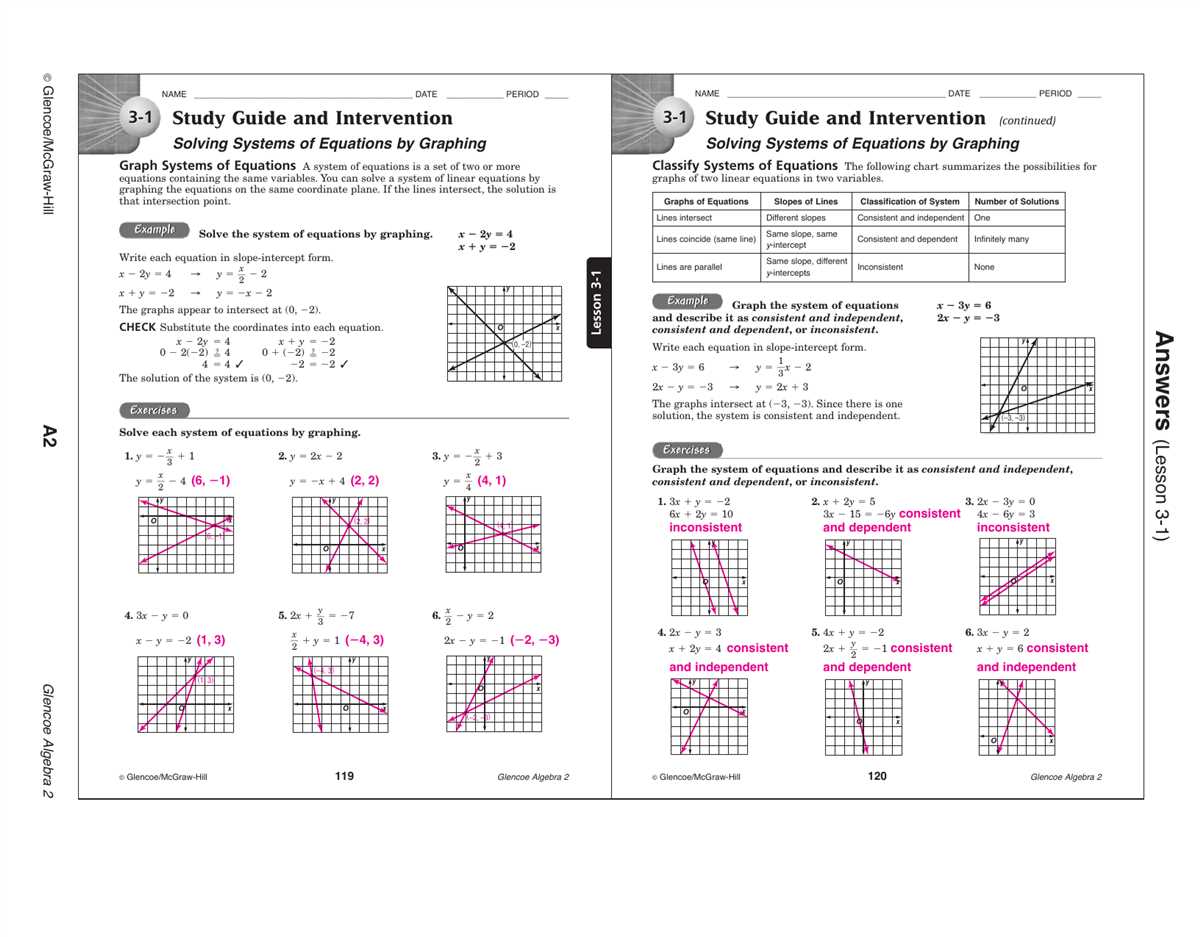
Solving Systems of Equations – Section 5.2

In Section 5.2, we learn the methods for solving systems of equations. A system of equations is a set of equations that are related to each other and have a common solution or solutions. Solving a system of equations involves finding the values of the variables that satisfy all of the equations in the system.
There are two main methods for solving systems of equations: the substitution method and the elimination method. In the substitution method, we solve one equation for one variable and substitute that expression into the other equation. This allows us to eliminate one variable and solve for the other. The elimination method involves adding or subtracting the equations to eliminate one variable and solve for the other.
When solving systems of equations, it is important to understand the concept of consistency. A consistent system has at least one solution, while an inconsistent system has no solution. Additionally, a system can be classified as dependent or independent. A dependent system has infinitely many solutions, while an independent system has a unique solution.
Throughout Section 5.2, we will practice solving systems of equations using both the substitution and elimination methods. We will also learn how to classify systems as consistent or inconsistent, and dependent or independent. This knowledge will be crucial as we continue to solve more complex systems of equations in later sections.
Methods for Solving Systems of Equations
In algebra, a system of equations refers to a set of two or more equations with multiple variables. These equations are typically solved simultaneously to determine the values of the variables that satisfy all the equations. There are several methods for solving systems of equations, some of which include:
- Substitution Method: This method involves solving one equation for one variable and then substituting the expression into the other equation. By substituting the expression, a single equation with a single variable is obtained, which can be easily solved to find the value of that variable.
- Elimination Method: The elimination method, also known as the addition or subtraction method, involves adding or subtracting the equations in a system to eliminate one variable. By performing the necessary operations, a new equation with one less variable is obtained. This process is repeated until only one variable remains, which can be solved to find its value.
- Matrix Method: The matrix method uses matrices to represent the system of equations. The coefficients of the variables in the equations are placed in a matrix, and the values on the right side of the equations are placed in another matrix. By performing matrix operations, such as row operations, the system of equations can be transformed into an equivalent system with an easier form. The values of the variables can then be determined by solving the transformed system.
- Graphing Method: This method involves graphing the equations on a coordinate plane and finding the point of intersection. The coordinates of the intersection point represent the solution to the system of equations. This method is particularly useful when the equations are linear and can be easily graphed.
These are just a few of the methods for solving systems of equations. The choice of method depends on the specific characteristics of the equations and the preferences of the mathematician. By using these methods, mathematicians can efficiently find the solutions to systems of equations, which have a wide range of applications in various fields.
Section 5.3: Exponents and Exponential Functions

Exponents and exponential functions play a crucial role in algebra 2. In this section, we will explore the properties of exponents and how they relate to exponential functions. Exponential functions have a base raised to a variable exponent, and they often represent growth or decay situations.
Properties of Exponents: When working with exponents, there are several important properties to keep in mind. One property states that any number raised to the power of zero is equal to one. Another property states that when multiplying powers with the same base, you can add the exponents. And when dividing powers with the same base, you can subtract the exponents.
Example: If you have 5^3 * 5^2, you can add the exponents to get 5^(3+2) = 5^5. Similarly, if you have 4^7 / 4^3, you can subtract the exponents to get 4^(7-3) = 4^4.
Exponential Functions: An exponential function is a function of the form f(x) = a * b^x, where a is a constant and b is the base of the exponential function. The base determines whether the exponential function represents growth or decay. If b > 1, the function represents exponential growth, and if 0 < b < 1, the function represents exponential decay.
Example: The function f(x) = 2 * 3^x represents exponential growth, where the base is 3. As x increases, the function gets larger exponentially. On the other hand, the function g(x) = 5 * (1/2)^x represents exponential decay, where the base is 1/2. As x increases, the function gets smaller exponentially.
Graphical Representation: Exponential functions have distinct graphical representations. When the base is greater than 1, the graph of the function starts at the y-intercept and rises exponentially. When the base is between 0 and 1, the graph starts at the y-intercept and decreases exponentially. The rate of growth or decay depends on the value of the base.
Example: The graph of the exponential function f(x) = 2 * 3^x starts at the y-intercept, which is at (0, 2), and rises rapidly as x increases. The graph of the exponential function g(x) = 5 * (1/2)^x starts at the y-intercept, which is at (0, 5), and decays rapidly as x increases.
Applications: Exponential functions are used in various real-world applications, including population growth, compound interest, and radioactive decay. Understanding exponential functions can help us analyze and model these situations accurately.
Example: The population of a city can be modeled by an exponential function, where the base represents the growth rate. By studying the exponential function, we can make predictions about future population trends and plan accordingly.