
In geometry, the study of shapes and their properties is crucial for understanding and solving various mathematical problems. One important topic is the calculation of areas for parallelograms and triangles. These two-dimensional figures can occur in various real-world situations, such as architecture or engineering, where accurate measurements and precise calculations are necessary.
Glencoe Geometry is a comprehensive textbook that provides students with the necessary knowledge and skills to excel in the field of geometry. Chapter 11, titled “Areas of Parallelograms and Triangles,” focuses specifically on the calculation of areas for these two types of polygons. The chapter includes various exercises and problems to reinforce the concepts and enable students to practice their skills.
The 11-1 skills practice section of Glencoe Geometry provides answers to the exercises in this chapter. By having access to these answers, students can check their work, identify any mistakes, and learn from them. This helps to enhance their understanding of the concepts and improve their problem-solving abilities. Furthermore, the answers serve as a valuable study aid, providing additional examples and solutions to further clarify the methods and techniques used.
Overall, the 11-1 skills practice areas of parallelograms and triangles answers in Glencoe Geometry play a crucial role in supporting effective learning and mastery of the subject. With these answers, students can confidently tackle exercises, practice their skills, and gain a deeper understanding of the calculations involved in determining the areas of parallelograms and triangles.
Overview of the topic
The topic of “11-1 skills practice areas of parallelograms and triangles” in Glencoe Geometry focuses on understanding and applying the formulas for finding the areas of parallelograms and triangles. This topic is important in geometry as it provides the foundation for solving more complex problems involving shapes and their areas.
In this section, students will learn about the properties of parallelograms and triangles, including their angles, sides, and diagonals. They will also learn how to apply the formulas for finding the area of a parallelogram and a triangle based on their given measurements.
The skills and concepts covered in this topic include calculating the area of a parallelogram using the base and height, calculating the area of a triangle using the base and height, as well as using the properties of special parallelograms and triangles to find their areas. Students will also learn how to solve real-life problems involving these shapes and their areas.
This topic is essential for developing a solid understanding of geometry and its applications. It provides students with the tools and knowledge necessary to solve more complex problems in geometry and other related fields, such as engineering and architecture. Mastering the skills in this topic will also prepare students for further studies in advanced geometry and trigonometry.
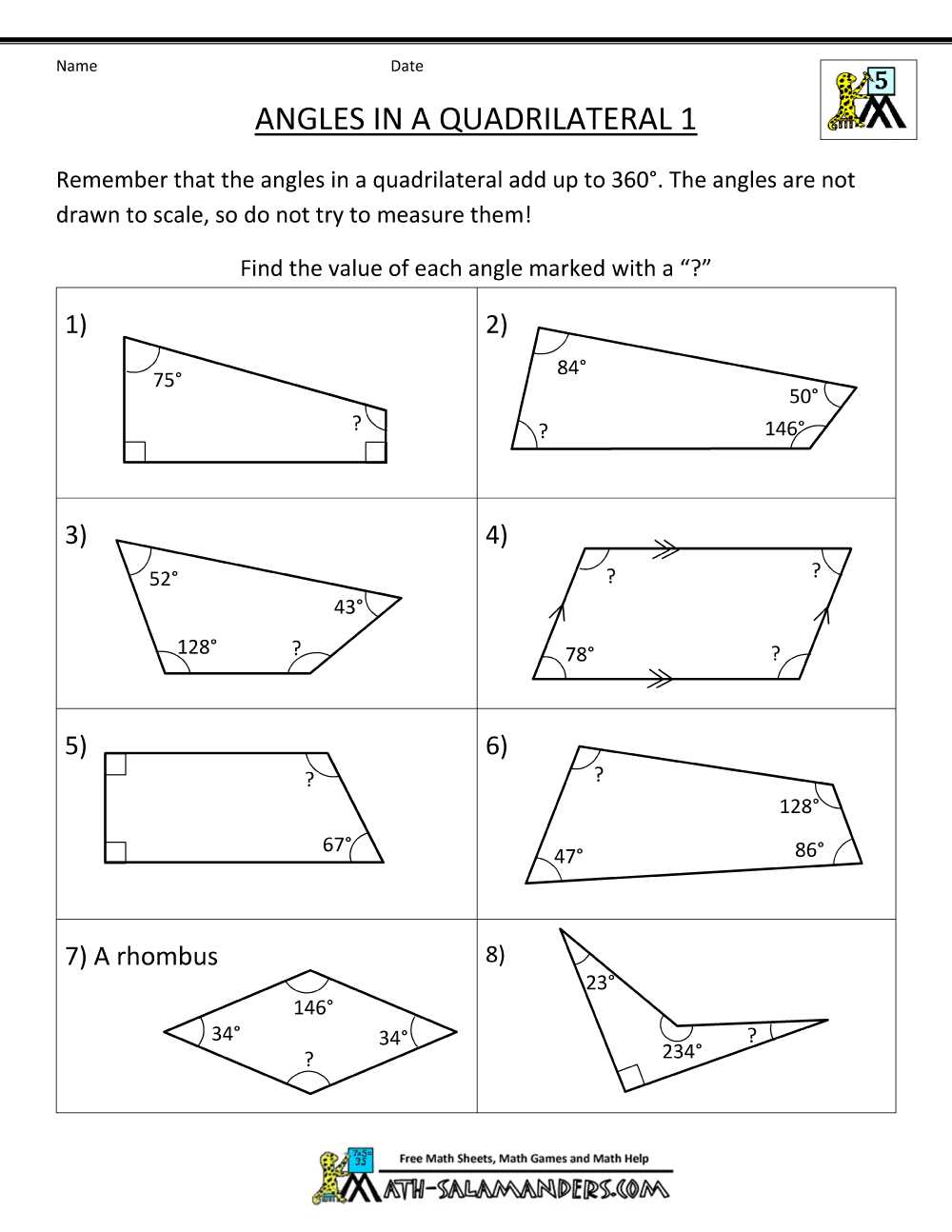
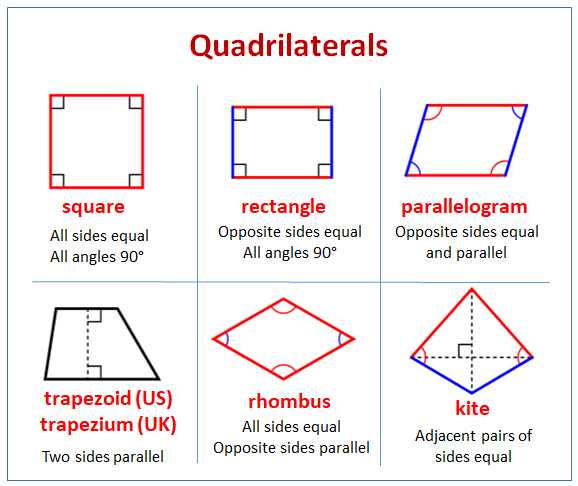
What is a parallelogram?
A parallelogram is a quadrilateral with two pairs of parallel sides. This means that opposite sides are parallel and equal in length. The parallel sides are often referred to as the base and the top, and the other two sides are called the legs or the sides.
The angles in a parallelogram are also important. Opposite angles of a parallelogram are congruent, meaning they have the same measure. Additionally, the consecutive angles in a parallelogram are supplementary, meaning they add up to 180 degrees.
In terms of properties, a parallelogram has several key characteristics. The diagonals of a parallelogram bisect each other, meaning they divide each other equally. The diagonals also divide the parallelogram into four congruent triangles. The area of a parallelogram can be calculated by multiplying the base by the height, where the height is the perpendicular distance between the base and the top.
Overall, a parallelogram is a versatile geometric shape that has many interesting properties. Its parallel sides and congruent angles make it a useful tool for various mathematical calculations and applications.
Definition and Properties of Parallelograms
A parallelogram is a quadrilateral with two pairs of parallel sides. In other words, opposite sides of a parallelogram are parallel. This means that if we take any two sides of a parallelogram, they will never intersect, no matter how far they are extended.
One of the important properties of parallelograms is that opposite sides are congruent, which means they have the same length. This can be proven using the properties of parallel lines and transversals. Another property of parallelograms is that opposite angles are congruent. This means that if we take any two opposite angles of a parallelogram, they will have the same measure.
Additionally, the diagonals of a parallelogram bisect each other. This means that if we draw the two diagonals of a parallelogram, they will intersect at a point that divides each diagonal into two equal segments. The diagonals of a parallelogram also divide it into four congruent triangles.
One more important property of parallelograms is that the consecutive angles are supplementary. This means that if we take any two consecutive angles of a parallelogram, their measures add up to 180 degrees.
In summary, parallelograms have two pairs of parallel sides, opposite sides and angles are congruent, diagonals bisect each other and divide the parallelogram into congruent triangles, and consecutive angles are supplementary.
Examples of parallelograms
Parallelograms are quadrilaterals with opposite sides parallel and equal in length. They have several unique properties that distinguish them from other shapes.
1. Rectangle: A rectangle is a type of parallelogram with four right angles. Its opposite sides are parallel and equal in length. In a rectangle, the diagonals are also congruent and bisect each other at a right angle.
2. Rhombus: A rhombus is a parallelogram with four equal sides. Its opposite sides are parallel and opposite angles are also equal. The diagonals of a rhombus bisect each other at a 90-degree angle.
3. Square: A square is a special type of rectangle and rhombus. It has all the properties of both shapes – four right angles, congruent sides, and diagonals that bisect each other at a right angle. The unique property of a square is that all of its sides are equal in length.
4. Trapezoid: A trapezoid is another type of quadrilateral that has one pair of opposite sides parallel. However, unlike a parallelogram, its other pair of opposite sides are not parallel. The two non-parallel sides are called the legs, while the parallel sides are known as the bases.
5. Kite: A kite is a quadrilateral with two pairs of adjacent sides equal in length. It is not a parallelogram since its opposite sides are not parallel. The diagonals of a kite are perpendicular, and one diagonal bisects the other.
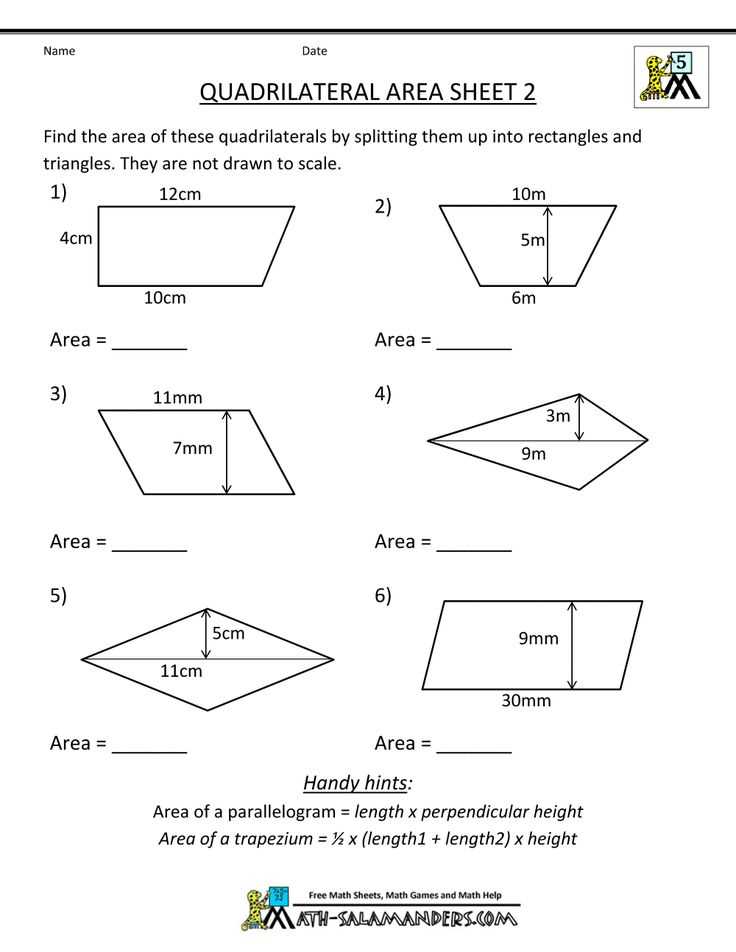
Finding the area of a parallelogram

A parallelogram is a four-sided polygon in which opposite sides are parallel. To find the area of a parallelogram, you need to know the length of the base and the height. The base is one of the parallel sides, and the height is the perpendicular distance between the base and the opposite side.
To calculate the area, you can use the formula: Area = base × height. The length of the base is usually given or can be measured, and the height can be determined by drawing a perpendicular line from the base to the opposite side.
Another method to find the area of a parallelogram is to use the lengths of the diagonals. If the lengths of the diagonals are given, you can use the formula: Area = (1/2) × product of the diagonals.
It’s important to note that the units for the base and height should be the same, such as centimeters or inches, to ensure accurate results. Additionally, make sure to double-check your calculations and use the appropriate units when reporting the area.
In conclusion, finding the area of a parallelogram requires knowledge of the base and height or the lengths of the diagonals. By applying the appropriate formulas and double-checking your calculations, you can accurately determine the area of a parallelogram.
Formulas for calculating the area of a parallelogram
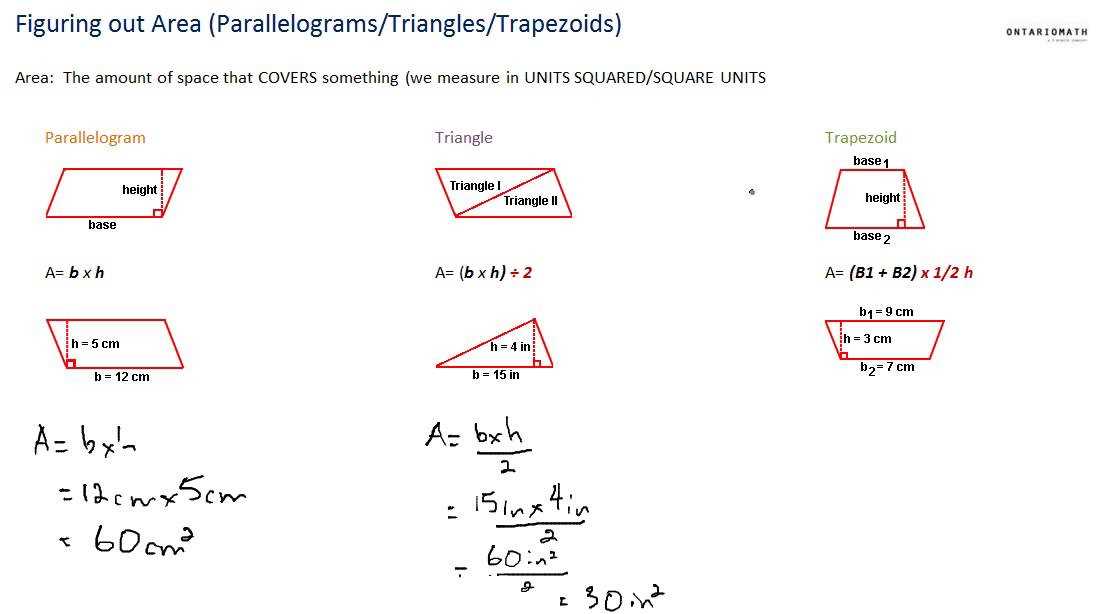
A parallelogram is a four-sided polygon with opposite sides that are parallel and equal in length. It is a useful shape in geometry, and finding its area can be done using a simple formula.
The formula for calculating the area of a parallelogram is:
Area = base × height
The base of a parallelogram is any of its sides, and the height is the perpendicular distance between the base and the opposite side. To find the area, you multiply the base by the height.
Another way to calculate the area of a parallelogram is by using the lengths of its sides and one of its angles. The formula is:
Area = side length × side length × sin(angle)
This formula uses the sine of the angle between two adjacent sides of the parallelogram to find the area. The side length is multiplied by itself, and then multiplied by the sine of the angle to get the final area.
These formulas come in handy when working with parallelograms, whether it’s finding the area of a shape or solving problems involving their properties. Understanding how to calculate the area of a parallelogram is an essential skill in geometry.
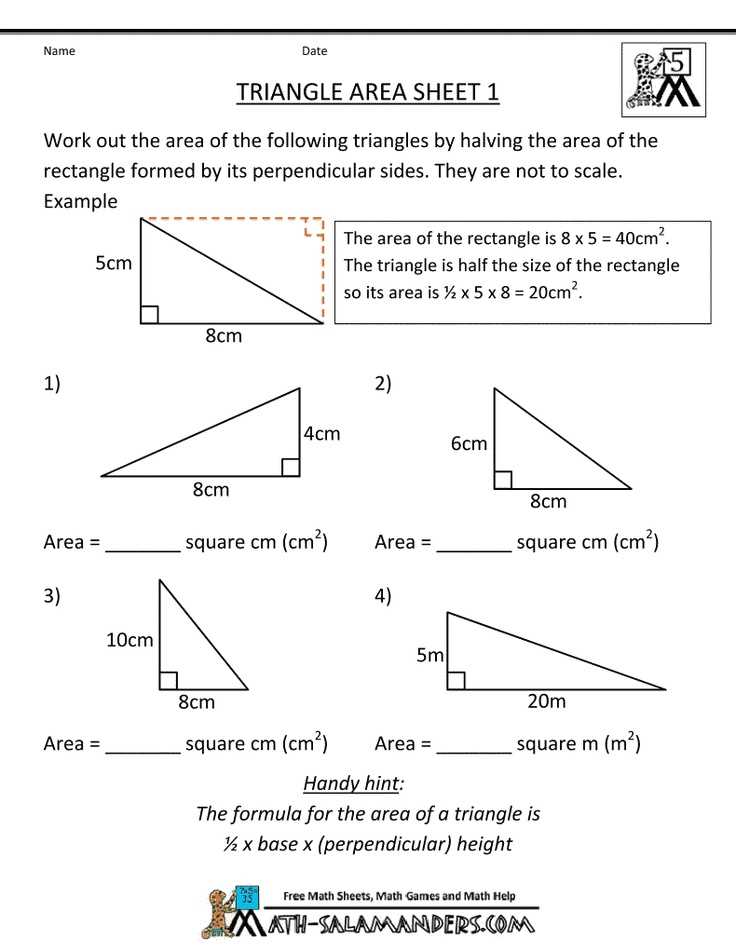
Step-by-step examples and practice problems
A thorough understanding of the concepts and formulas related to areas of parallelograms and triangles is crucial in geometry. To help students grasp these concepts effectively, step-by-step examples and practice problems are essential.
Step-by-step examples provide a clear and organized approach to solving problems. They break down complex problems into smaller, more manageable steps, making it easier for students to follow along and understand the reasoning behind each step. These examples often include explanations of the formulas used and the properties of parallelograms and triangles that are relevant to the problem at hand.
Practice problems are an integral part of learning, as they allow students to apply the knowledge they have gained from the examples. These problems vary in difficulty, ranging from simple calculations of areas to more complex problems involving multiple shapes and concepts. By practicing a variety of problems, students can build their problem-solving skills and reinforce their understanding of the formulas and concepts.
One effective way to incorporate step-by-step examples and practice problems is through a textbook or online resource. These resources typically include a mix of examples with detailed solutions and practice problems for students to attempt on their own. Additionally, online platforms may offer interactive features that allow students to get immediate feedback on their answers and track their progress.
By providing step-by-step examples and practice problems, educators can give students the tools they need to master the concepts and formulas related to areas of parallelograms and triangles. With consistent practice, students can develop their problem-solving skills and gain confidence in their ability to apply geometry concepts to real-world scenarios.
What is a triangle?
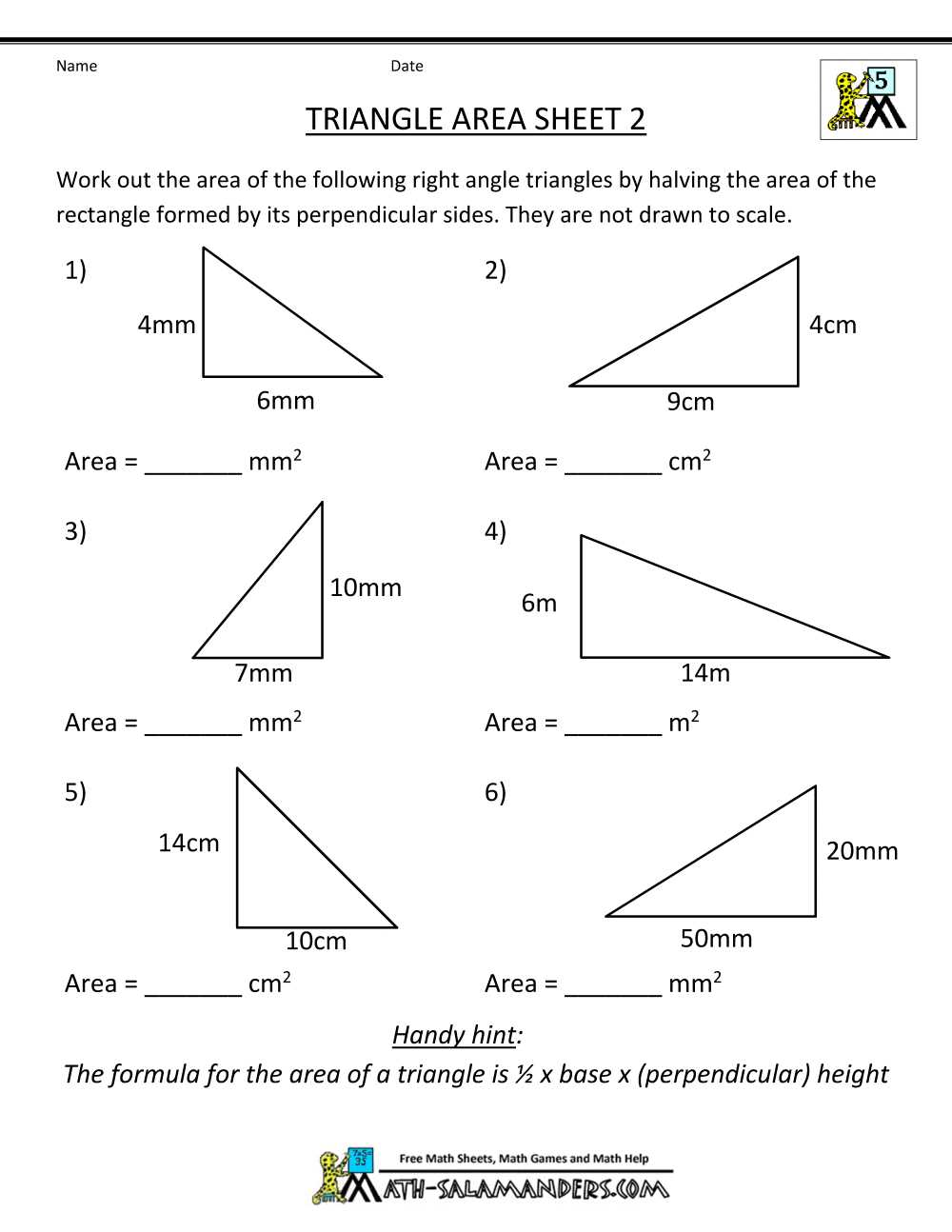
A triangle is a polygon with three sides and three angles. It is one of the basic shapes in geometry and is formed by connecting three non-collinear points. Each side of a triangle connects two vertices, and each angle is formed by two adjacent sides.
Triangles can be classified based on the lengths of their sides and the measures of their angles. There are several types of triangles, including equilateral, isosceles, and scalene triangles, which differ in their side lengths. Equilateral triangles have three congruent sides, isosceles triangles have at least two congruent sides, and scalene triangles have no congruent sides.
Triangles can also be classified based on their angles. Acute triangles have all three angles measuring less than 90 degrees, obtuse triangles have one angle measuring more than 90 degrees, and right triangles have one angle measuring exactly 90 degrees. Additionally, triangles can be classified as equiangular if all three angles are congruent.
Definition and Properties of Triangles
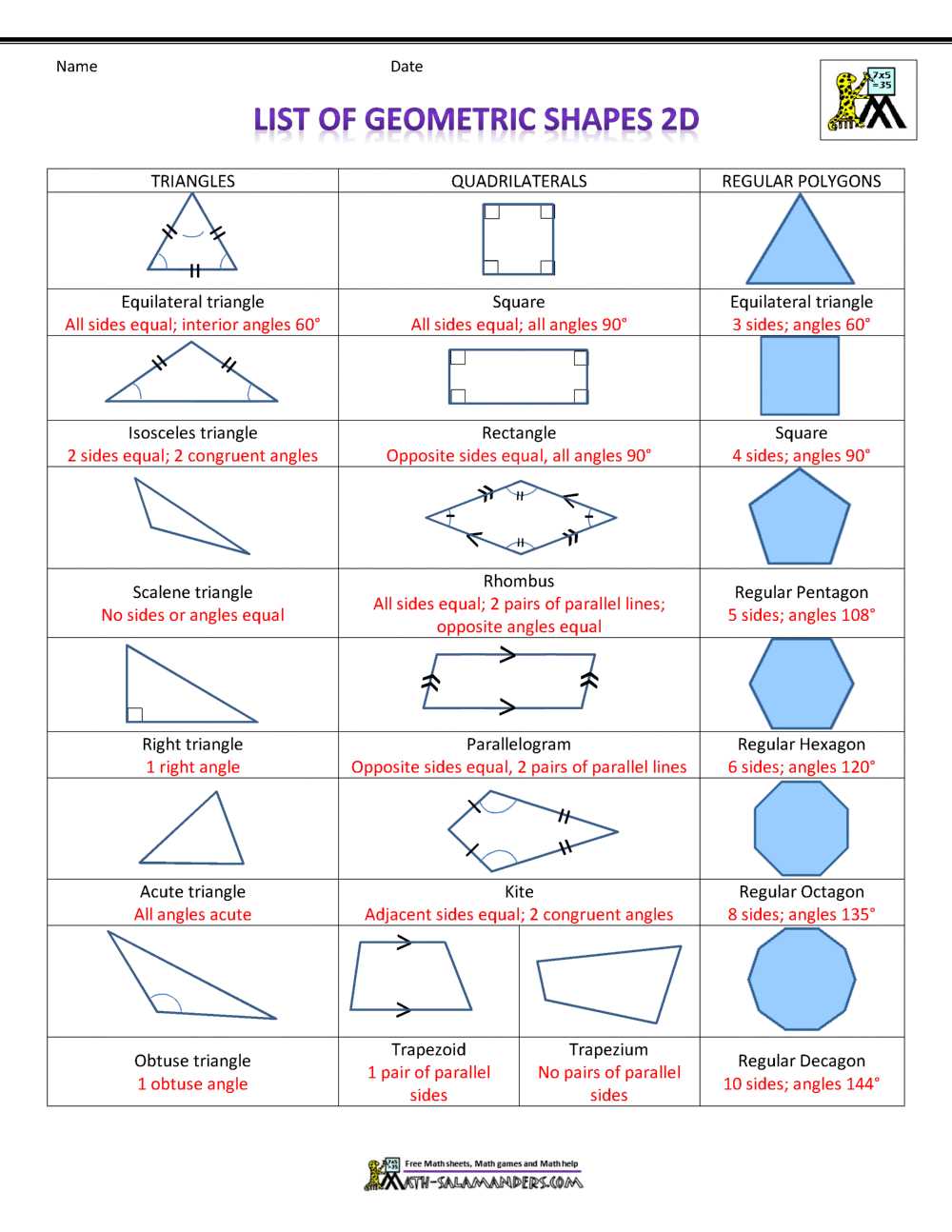
A triangle is a polygon with three sides, three vertices, and three angles. It is one of the most basic and fundamental shapes in geometry. Triangles can be classified into different types based on the length of their sides and the size of their angles.
Types of Triangles:
- Equilateral Triangle: An equilateral triangle is a triangle with all three sides of equal length. Each angle in an equilateral triangle measures 60 degrees.
- Isosceles Triangle: An isosceles triangle is a triangle with at least two sides of equal length. The angles opposite the equal sides are also equal.
- Scalene Triangle: A scalene triangle is a triangle with all three sides of different lengths. The angles in a scalene triangle can be different as well.
- Right Triangle: A right triangle is a triangle that has one angle measuring 90 degrees. The side opposite the right angle is called the hypotenuse, and the other two sides are called the legs.
Properties of Triangles:
- Angle Sum Property: The sum of the three interior angles of any triangle is always 180 degrees.
- Side Length Property: In a triangle, the sum of the lengths of any two sides is always greater than the length of the third side.
- Congruent Triangles: Two triangles are congruent if their corresponding sides and angles are equal.
- Similar Triangles: Two triangles are similar if their corresponding angles are equal.
Understanding the definition and properties of triangles is essential in various areas of mathematics and real-life applications, such as geometry, trigonometry, and engineering.
Types of Triangles
Triangles are a fundamental shape in geometry, and there are different types of triangles based on their sides and angles. The classification of triangles is important for understanding their properties and relationships.
1. Equilateral Triangle
An equilateral triangle has three equal sides and three equal angles. Each angle measures 60 degrees, and all sides have the same length. It is the only type of triangle that is also an equiangular triangle.
2. Isosceles Triangle
An isosceles triangle has two equal sides and two equal angles. The angles opposite the equal sides are equal. The third side and angle are unequal. The base angles of an isosceles triangle are always equal.
3. Scalene Triangle
A scalene triangle has three unequal sides and three unequal angles. None of its angles are equal. The lengths of its sides and the measures of its angles are all different.
4. Right Triangle
A right triangle has one right angle, which measures 90 degrees. The side opposite the right angle is called the hypotenuse, and the other two sides are called the legs. The Pythagorean theorem is often used to find the lengths of the sides of a right triangle.
5. Obtuse Triangle
An obtuse triangle has one obtuse angle, which measures more than 90 degrees. The other two angles are acute angles, measuring less than 90 degrees.
6. Acute Triangle
An acute triangle has three acute angles, which each measure less than 90 degrees. All sides of an acute triangle are smaller in length than the sum of the two other sides.
Understanding the different types of triangles is essential for solving geometry problems and determining the properties of shapes in various contexts.